Difference between revisions of "Technical Aspects of Grid Interconnection"
***** (***** | *****) m |
***** (***** | *****) m (→References) |
||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = Overview - The Evolution of Interconnected Systems< | + | == Overview - The Evolution of Interconnected Systems<ref name="Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,">Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf, </ref>== |
Electricity grid interconnections have played a key role in the history of electric power systems. Most national and regional power systems that exist today began many decades ago as isolated systems, often as a single generator in a large city. As power systems expanded out from their urban cores, interconnections among neighboring systems became increasingly common<ref name="T. Hughes (983),Networks of Power: Electrification in Western Society, 1880-1930, Johns Hopkins University, Baltimore, MD">T. Hughes (983),Networks of Power: Electrification in Western Society, 1880-1930, Johns Hopkins University, Baltimore, MD</ref> . Groups of utilities began to form power pools, allowing them to trade electricity and share capacity reserves. The first power pool in the United States was formed in the Connecticut Valley in 1925<ref name="Rincliffe, R.G. (967), “Planning and Operation of a Large Power Pool.”.IEEE Spectrum: 9-96. January 967. The PJM (Pennsylvania/New Jersey/Maryland) grid was next to be developed, in 927.">Rincliffe, R.G. (967), “Planning and Operation of a Large Power Pool.”.IEEE Spectrum: 9-96. January 967. The PJM (Pennsylvania/New Jersey/Maryland) grid was next to be developed, in 927.</ref>.<br/> | Electricity grid interconnections have played a key role in the history of electric power systems. Most national and regional power systems that exist today began many decades ago as isolated systems, often as a single generator in a large city. As power systems expanded out from their urban cores, interconnections among neighboring systems became increasingly common<ref name="T. Hughes (983),Networks of Power: Electrification in Western Society, 1880-1930, Johns Hopkins University, Baltimore, MD">T. Hughes (983),Networks of Power: Electrification in Western Society, 1880-1930, Johns Hopkins University, Baltimore, MD</ref> . Groups of utilities began to form power pools, allowing them to trade electricity and share capacity reserves. The first power pool in the United States was formed in the Connecticut Valley in 1925<ref name="Rincliffe, R.G. (967), “Planning and Operation of a Large Power Pool.”.IEEE Spectrum: 9-96. January 967. The PJM (Pennsylvania/New Jersey/Maryland) grid was next to be developed, in 927.">Rincliffe, R.G. (967), “Planning and Operation of a Large Power Pool.”.IEEE Spectrum: 9-96. January 967. The PJM (Pennsylvania/New Jersey/Maryland) grid was next to be developed, in 927.</ref>.<br/> | ||
| Line 14: | Line 14: | ||
<br/> | <br/> | ||
| − | = General Potential Benefits of Grid Interconnections<ref name="http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf">http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf</ref> | + | == General Potential Benefits of Grid Interconnections<ref name="Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,">Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf, </ref>== |
There are number of technical rationales for grid interconnections, many of which have economic components as well.<br/> | There are number of technical rationales for grid interconnections, many of which have economic components as well.<br/> | ||
<u>Technical rationales for grid interconnection include:</u> | <u>Technical rationales for grid interconnection include:</u> | ||
| + | |||
*Improving reliability and pooling reserves: The amount of reserve capacity that must be built by individual networks to ensure reliable operation when supplies are short can be reduced by sharing reserves within an interconnected network. | *Improving reliability and pooling reserves: The amount of reserve capacity that must be built by individual networks to ensure reliable operation when supplies are short can be reduced by sharing reserves within an interconnected network. | ||
*Reduced investment in generating capacity: Individual systems can reduce their generating capacity requirement, or postpone the need to add new capacity, if they are able to share the generating resources of an interconnected system. | *Reduced investment in generating capacity: Individual systems can reduce their generating capacity requirement, or postpone the need to add new capacity, if they are able to share the generating resources of an interconnected system. | ||
| Line 26: | Line 27: | ||
*Economic exchange: Interconnection allows the dispatch of the least costly generating units within the interconnected area, providing an overall cost savings that can be divided among the component systems. Alternatively, it allows inexpensive power from one system to be sold to systems with more expensive power. | *Economic exchange: Interconnection allows the dispatch of the least costly generating units within the interconnected area, providing an overall cost savings that can be divided among the component systems. Alternatively, it allows inexpensive power from one system to be sold to systems with more expensive power. | ||
*Environmental dispatch and new plant siting: Interconnections can allow generating units with lower environmental impacts to be used more, and units with higher impacts to be used less. In areas where environmental and land use constraints limit the siting of power plants, interconnections can allow new plant construction in less sensitive areas. | *Environmental dispatch and new plant siting: Interconnections can allow generating units with lower environmental impacts to be used more, and units with higher impacts to be used less. In areas where environmental and land use constraints limit the siting of power plants, interconnections can allow new plant construction in less sensitive areas. | ||
| − | *Coordination of maintenance schedules: Interconnections permit planned outages of generating and transmission facilities for maintenance to be coordinated so that overall cost and reliability for the interconnected network is optimized. Some costs and benefits of interconnections are difficult to quantify, but as a rough figure of merit it has been estimated that interconnections in North America have resulted in an overall annual cost savings of $20 billion in the 1990s, and that the Western European interconnection has resulted in reduced capacity requirements of 7-10 %. | + | *Coordination of maintenance schedules: Interconnections permit planned outages of generating and transmission facilities for maintenance to be coordinated so that overall cost and reliability for the interconnected network is optimized. Some costs and benefits of interconnections are difficult to quantify, but as a rough figure of merit it has been estimated that interconnections in North America have resulted in an overall annual cost savings of $20 billion in the 1990s, and that the Western European interconnection has resulted in reduced capacity requirements of 7-10 %. |
<br/> | <br/> | ||
| − | = Technical Complexities and Risks of Grid Interconnections<ref name="http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf">http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf</ref> | + | == Technical Complexities and Risks of Grid Interconnections<ref name="Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,">Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf, </ref>== |
The fact that interconnections between power systems are increasingly common does not imply that they are as simple as connecting a few wires. Interconnections obviously entail the expense of constructing and operating transmission lines and substations, or in the case of HVDC, converter stations. Interconnections also entail other costs, technical complexities, and risks. For AC interconnections especially, a power system interconnection is a kind of marriage, because two systems become one in an important way when they operate in synchronism. To do this requires a high degree of technical compatibility and operational coordination, which grows in cost and complexity with the scale and inherent differences of the systems involved. To give just one example, when systems are interconnected, even if they are otherwise fully compatible, fault currents (the current that flows during a short circuit) generally increase, requiring the installation of higher capacity circuit breakers to maintain safety and reliability. To properly specify these and many other technical changes required by interconnection requires extensive planning studies, computer modeling, and exchange of data between the interconnected systems.<br/> | The fact that interconnections between power systems are increasingly common does not imply that they are as simple as connecting a few wires. Interconnections obviously entail the expense of constructing and operating transmission lines and substations, or in the case of HVDC, converter stations. Interconnections also entail other costs, technical complexities, and risks. For AC interconnections especially, a power system interconnection is a kind of marriage, because two systems become one in an important way when they operate in synchronism. To do this requires a high degree of technical compatibility and operational coordination, which grows in cost and complexity with the scale and inherent differences of the systems involved. To give just one example, when systems are interconnected, even if they are otherwise fully compatible, fault currents (the current that flows during a short circuit) generally increase, requiring the installation of higher capacity circuit breakers to maintain safety and reliability. To properly specify these and many other technical changes required by interconnection requires extensive planning studies, computer modeling, and exchange of data between the interconnected systems.<br/> | ||
| Line 42: | Line 43: | ||
The greatest benefits of interconnection are usually derived from synchronous AC operation, but this can also entail greater reliability risks. In any synchronous network, disturbances in one location are quickly felt in other locations. After interconnecting, a system that used to be isolated from disturbances in a neighboring system is now vulnerable to those disturbances. As major blackouts in North America and Europe in 2003 demonstrated, large-scale disturbances can propagate through interconnections and result in cascading outages, bringing down systems that had previously been functioning normally. In addition, long-distance interconnections with long transmission lines have potentially greater stability problems than is the case for shorter lines. Finally, many systems that have undergone electricity liberalization in recent years have experienced large increases in transmission capacity utilization, reducing reserve margins. Minimizing the likelihood that an interconnection will lead to such problems as voltage collapse, dynamic and transient instability, or cascading outages due to propagated disturbances requires careful planning and well-coordinated operation.<br/> | The greatest benefits of interconnection are usually derived from synchronous AC operation, but this can also entail greater reliability risks. In any synchronous network, disturbances in one location are quickly felt in other locations. After interconnecting, a system that used to be isolated from disturbances in a neighboring system is now vulnerable to those disturbances. As major blackouts in North America and Europe in 2003 demonstrated, large-scale disturbances can propagate through interconnections and result in cascading outages, bringing down systems that had previously been functioning normally. In addition, long-distance interconnections with long transmission lines have potentially greater stability problems than is the case for shorter lines. Finally, many systems that have undergone electricity liberalization in recent years have experienced large increases in transmission capacity utilization, reducing reserve margins. Minimizing the likelihood that an interconnection will lead to such problems as voltage collapse, dynamic and transient instability, or cascading outages due to propagated disturbances requires careful planning and well-coordinated operation.<br/> | ||
| − | + | == Technical Parameters of Interconnection<ref name="Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,">Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf, </ref>== | |
| − | |||
| − | = Technical Parameters of Interconnection<ref name="http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf">http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf</ref> | ||
| − | == Basic Electrical Parameters | + | === Basic Electrical Parameters === |
This section describes the basic electrical parameters and units of measurement used in electric power systems. It is meant to provide the non-technical reader with the concepts needed for a general understanding of the technical issues discussed in subsequent sections. | This section describes the basic electrical parameters and units of measurement used in electric power systems. It is meant to provide the non-technical reader with the concepts needed for a general understanding of the technical issues discussed in subsequent sections. | ||
| Line 52: | Line 51: | ||
<br/> | <br/> | ||
| − | == Alternating Current (AC) and Direct Current (DC) | + | === Alternating Current (AC) and Direct Current (DC) === |
| + | |||
| + | Electric power comes in two forms: | ||
| + | |||
| + | *'''alternating current (AC)''' and | ||
| + | *'''direct current (DC)'''. | ||
| − | + | These forms are characterized by the behavior of their waveforms: AC alternates between positive and negative polarity with respect to ground, while DC does not. | |
In power systems, AC is generally a sine wave, while DC is a constant value. Early electricity systems, such as Thomas Edison’s Pearl Street Station in New York City, which provided the world’s first public electric service in 1882, were DC. However, by the beginning of the 20th century AC systems had become standard worldwide. The main reason for the adoption of AC was that it is relatively simple to change AC voltage levels by using transformers, while it is difficult to change DC voltages. The development of solid-state power electronics in recent years has allowed an increased use of DC in the form of HVDC interconnections, but otherwise power systems remain AC. | In power systems, AC is generally a sine wave, while DC is a constant value. Early electricity systems, such as Thomas Edison’s Pearl Street Station in New York City, which provided the world’s first public electric service in 1882, were DC. However, by the beginning of the 20th century AC systems had become standard worldwide. The main reason for the adoption of AC was that it is relatively simple to change AC voltage levels by using transformers, while it is difficult to change DC voltages. The development of solid-state power electronics in recent years has allowed an increased use of DC in the form of HVDC interconnections, but otherwise power systems remain AC. | ||
| − | <br/> | + | <br/><br /> |
| − | == Frequency (Hz) | + | === Frequency (Hz) === |
Frequency is the rate at which an alternating current changes from positive to negative polarity, measured in cycles per second, or '''hertz (Hz)'''. There are currently two widespread world standards for power system frequency: 50 Hz in most of Europe and Asia, and 60 Hz in North America and in other places strongly influenced by the U.S. power industry, such as South Korea. The choice of 50 and 60 Hz systems in different locations is a consequence of historical legacies rather than the inherent technical superiority of one or the other. However, the range of possible frequencies for power systems is constrained by practical concerns. For example, a century ago many electric railroads operated at a frequency of 25 Hz, but 25 Hz was never adopted for general use in power systems because frequencies at that level cause electric lights to flicker. At the other end of the scale, frequencies well above 60 Hz result in higher impedances, leading to unacceptably high transmission and distribution losses. | Frequency is the rate at which an alternating current changes from positive to negative polarity, measured in cycles per second, or '''hertz (Hz)'''. There are currently two widespread world standards for power system frequency: 50 Hz in most of Europe and Asia, and 60 Hz in North America and in other places strongly influenced by the U.S. power industry, such as South Korea. The choice of 50 and 60 Hz systems in different locations is a consequence of historical legacies rather than the inherent technical superiority of one or the other. However, the range of possible frequencies for power systems is constrained by practical concerns. For example, a century ago many electric railroads operated at a frequency of 25 Hz, but 25 Hz was never adopted for general use in power systems because frequencies at that level cause electric lights to flicker. At the other end of the scale, frequencies well above 60 Hz result in higher impedances, leading to unacceptably high transmission and distribution losses. | ||
| Line 66: | Line 70: | ||
<br/> | <br/> | ||
| − | == Voltage (V) | + | === Voltage (V) === |
Voltage is the difference in electric potential between two points in an electric circuit. A difference in potential causes electric charges to flow from one place to another, just as a difference in heights causes water to flow from one level to another. Voltage is measured in '''volts (V)''', and sometimes in thousands of volts or kilovolts (kV). In power systems, two important measures are the maximum voltage and average voltage at any particular point. Maximum voltage is important because insulation and safety equipment must be designed to protect against the highest voltage encountered. Average voltage is important because the amount of energy supplied to an end user or lost in transmission lines is a function of the average voltage and current. For DC systems, maximum and average voltages are the same, because DC voltage doesn’t oscillate. For example, the output of a 120 V DC power supply is a continuous 120 V relative to ground, and this is both the maximum and average voltage. For AC systems, different measures are required. In a 120 V AC system, the voltage actually oscillates in a sine wave between + 170 V and – 170 V relative to ground. The maximum voltage, also called amplitude or peak voltage, is thus 170 V. The simple arithmetic average of this waveform is actually 0 V, since the positive and negative voltages cancel each other out. Hence, another type of average is used, called '''root-mean-square (RMS)'''. RMS is obtained by squaring the values of the voltage over one complete sine-wave cycle, determining its average value, and then taking the square root of that average. The result (true for any sine wave) is that VRMS = VPEAK / √2 = 0.707 VPEAK. For a household system with a VPEAK = 170 V, VRMS = 0.707 (170 V) = 120 V. Thus the common designation of a household electric outlet as “120 V AC” refers to the RMS value of the voltage. The voltages of power system components, such as transformers and transmission lines, are also generally given in RMS terms. | Voltage is the difference in electric potential between two points in an electric circuit. A difference in potential causes electric charges to flow from one place to another, just as a difference in heights causes water to flow from one level to another. Voltage is measured in '''volts (V)''', and sometimes in thousands of volts or kilovolts (kV). In power systems, two important measures are the maximum voltage and average voltage at any particular point. Maximum voltage is important because insulation and safety equipment must be designed to protect against the highest voltage encountered. Average voltage is important because the amount of energy supplied to an end user or lost in transmission lines is a function of the average voltage and current. For DC systems, maximum and average voltages are the same, because DC voltage doesn’t oscillate. For example, the output of a 120 V DC power supply is a continuous 120 V relative to ground, and this is both the maximum and average voltage. For AC systems, different measures are required. In a 120 V AC system, the voltage actually oscillates in a sine wave between + 170 V and – 170 V relative to ground. The maximum voltage, also called amplitude or peak voltage, is thus 170 V. The simple arithmetic average of this waveform is actually 0 V, since the positive and negative voltages cancel each other out. Hence, another type of average is used, called '''root-mean-square (RMS)'''. RMS is obtained by squaring the values of the voltage over one complete sine-wave cycle, determining its average value, and then taking the square root of that average. The result (true for any sine wave) is that VRMS = VPEAK / √2 = 0.707 VPEAK. For a household system with a VPEAK = 170 V, VRMS = 0.707 (170 V) = 120 V. Thus the common designation of a household electric outlet as “120 V AC” refers to the RMS value of the voltage. The voltages of power system components, such as transformers and transmission lines, are also generally given in RMS terms. | ||
| Line 72: | Line 76: | ||
<br/> | <br/> | ||
| − | == Current (I) | + | === Current (I) === |
Current is the flow rate of electric charge. In an electric circuit, charge flows from a point of higher voltage to a point of lower voltage through a conductor, just as water flows from a higher spot to a lower one through a pipe. Current is measured in'''amperes (A)''' or '''kilo-amperes (kA)''', where one ampere is a certain number of charges (to be precise 6.25 x 1018 charges, called one coulomb) flowing per second. As is the case for voltage, AC currents are generally described in terms of their RMS values. | Current is the flow rate of electric charge. In an electric circuit, charge flows from a point of higher voltage to a point of lower voltage through a conductor, just as water flows from a higher spot to a lower one through a pipe. Current is measured in'''amperes (A)''' or '''kilo-amperes (kA)''', where one ampere is a certain number of charges (to be precise 6.25 x 1018 charges, called one coulomb) flowing per second. As is the case for voltage, AC currents are generally described in terms of their RMS values. | ||
| Line 78: | Line 82: | ||
<br/> | <br/> | ||
| − | == Resistance (R) and Conductance | + | === Resistance (R) and Conductance === |
Conductance describes the ability of an object, such as an electric wire, to allow electric currents to flow. The reciprocal of conductance is resistance, which describes how much the object resists the flow of current. Resistance is measured in '''ohms (Ω)'''. The resistance of wire is a product of its resistivity (an inherent property of the material from which it is made, such as copper or aluminum, for a given temperature) and the dimensions of the wire. For a given material, the longer the wire is, the greater the resistance, and the larger in diameter the wire is, the smaller the resistance. In the analogy of water flowing from a higher to a lower spot through a pipe, resistance is analogous to the friction of the pipe. A narrow pipe has a higher resistance; a wide pipe has a lower resistance. | Conductance describes the ability of an object, such as an electric wire, to allow electric currents to flow. The reciprocal of conductance is resistance, which describes how much the object resists the flow of current. Resistance is measured in '''ohms (Ω)'''. The resistance of wire is a product of its resistivity (an inherent property of the material from which it is made, such as copper or aluminum, for a given temperature) and the dimensions of the wire. For a given material, the longer the wire is, the greater the resistance, and the larger in diameter the wire is, the smaller the resistance. In the analogy of water flowing from a higher to a lower spot through a pipe, resistance is analogous to the friction of the pipe. A narrow pipe has a higher resistance; a wide pipe has a lower resistance. | ||
| − | + | === Ohm’s Law === | |
| − | |||
| − | == Ohm’s Law == | ||
Ohm’s Law describes the relationship between voltage (V), current (I), and resistance (R) across any element of a DC electric circuit: V = I∗R. Thus, for a fixed value of resistance – say for an HVDC transmission line of a certain length and diameter – if the voltage is made larger, the current will decrease, and vice versa. For example, if the resistance of a line is 25 Ω, and the current through the line is 1 kA, then the voltage drop across the line is V = 1 kA * 25 Ω = 25 kV. If the voltage on the sending side was 500 kV, then the voltage on the receiving side must be 25 kV less, or 475 kV. | Ohm’s Law describes the relationship between voltage (V), current (I), and resistance (R) across any element of a DC electric circuit: V = I∗R. Thus, for a fixed value of resistance – say for an HVDC transmission line of a certain length and diameter – if the voltage is made larger, the current will decrease, and vice versa. For example, if the resistance of a line is 25 Ω, and the current through the line is 1 kA, then the voltage drop across the line is V = 1 kA * 25 Ω = 25 kV. If the voltage on the sending side was 500 kV, then the voltage on the receiving side must be 25 kV less, or 475 kV. | ||
| Line 90: | Line 92: | ||
<br/> | <br/> | ||
| − | == Power and Energy | + | === Power and Energy === |
Power is the rate of energy flow, measured in '''watts (W)''', and sometimes in thousands of watts or kilowatts (kW), or in millions of watts or megawatts (MW). For a DC circuit, the power passing through any element of the circuit (e.g. a transmission line, a generator, an electrical appliance) is the product of the voltage across it and the current passing through it: P = I∗V. The energy delivered by a power system is measured in kilowatt-hours (kWh), and sometimes megawatthours (MWh). In general, energy is equal to power times time. For example, a light bulb that draws 100 W of power and is in use for 10 hours consumes a total amount of energy, E = 0.1 kW * 10 h = 1 kWh. Note that power and energy are quite different concepts. If an electric oven draws 1 kW of power and is in use for an hour, E = 1 kW * 1 h = 1 kWh. In these two examples, the power levels are different but the energy consumed is the same, the difference being the length of time that each device is operated. Note that the basic unit of energy is the joule (J), while the basic unit of power is the watt, where 1 W = 1 J/s. Thus 1 kWh = 1 kW * 1 h = 1000 J/s * 3600 s = 3.6 million J. | Power is the rate of energy flow, measured in '''watts (W)''', and sometimes in thousands of watts or kilowatts (kW), or in millions of watts or megawatts (MW). For a DC circuit, the power passing through any element of the circuit (e.g. a transmission line, a generator, an electrical appliance) is the product of the voltage across it and the current passing through it: P = I∗V. The energy delivered by a power system is measured in kilowatt-hours (kWh), and sometimes megawatthours (MWh). In general, energy is equal to power times time. For example, a light bulb that draws 100 W of power and is in use for 10 hours consumes a total amount of energy, E = 0.1 kW * 10 h = 1 kWh. Note that power and energy are quite different concepts. If an electric oven draws 1 kW of power and is in use for an hour, E = 1 kW * 1 h = 1 kWh. In these two examples, the power levels are different but the energy consumed is the same, the difference being the length of time that each device is operated. Note that the basic unit of energy is the joule (J), while the basic unit of power is the watt, where 1 W = 1 J/s. Thus 1 kWh = 1 kW * 1 h = 1000 J/s * 3600 s = 3.6 million J. | ||
| Line 96: | Line 98: | ||
<br/> | <br/> | ||
| − | == Resistive Losses == | + | === Resistive Losses === |
When current flows against a resistance, some of its energy is lost in the form of heating. For a DC circuit, the resistive losses can be calculated using Ohm’s Law: PLOSS = I∗V = I(I/R) = I2R. To continue with the example under “Ohm’s Law” above, consider a 500 kV HVDC transmission line with 25 Ω of resistance, with 1 kA of current passing through it, and which has a voltage on the sending end of 500 kV, and a voltage on the receiving end of 475 kV. The total power being transmitted at the sending end of the transmission line is P = 500 kV ∗ 1 kA = 500 MW. Out of this 500 MW, the amount being lost to heating is PLOSS = (1 kA)2 ∗ 25 Ω = 25 MW. This constitutes 25 MW/500 MW = 5 percent of the power being transmitted. Very high voltages are used in transmission in order to reduce resistive losses to a tolerable level. In the example above, if the same amount of power were being transmitted (500 MW) but the sending voltage were 125 kV instead of 500 kV, the current through the line must be I = P/V = 500 MW/125 kV = 4 kA; the current is four times higher to yield the same amount of power, because the voltage is four times less. The power lost in the transmission line is then PLOSS = (4 kA)2 ∗ 25 Ω = 400 MW = 80 percent of the power being transmitted. In general, line losses are inversely proportional to the square of the sending voltage; this is true for AC lines as well as DC. For this reason, historically power systems have sought to increase their transmission voltages as distances and amounts of power transmitted have grown. The highest common AC transmission voltages, sometimes referred to as extra high voltage (EHV), are 380 kV in Europe and 765 kV in the US. Voltages as high as 1200 kV have been used in Russia for some long-distance lines across Siberia. Above 1000 kV, however, the practical difficulty and expense of equipment and insulation that can withstand such high voltages becomes prohibitive. | When current flows against a resistance, some of its energy is lost in the form of heating. For a DC circuit, the resistive losses can be calculated using Ohm’s Law: PLOSS = I∗V = I(I/R) = I2R. To continue with the example under “Ohm’s Law” above, consider a 500 kV HVDC transmission line with 25 Ω of resistance, with 1 kA of current passing through it, and which has a voltage on the sending end of 500 kV, and a voltage on the receiving end of 475 kV. The total power being transmitted at the sending end of the transmission line is P = 500 kV ∗ 1 kA = 500 MW. Out of this 500 MW, the amount being lost to heating is PLOSS = (1 kA)2 ∗ 25 Ω = 25 MW. This constitutes 25 MW/500 MW = 5 percent of the power being transmitted. Very high voltages are used in transmission in order to reduce resistive losses to a tolerable level. In the example above, if the same amount of power were being transmitted (500 MW) but the sending voltage were 125 kV instead of 500 kV, the current through the line must be I = P/V = 500 MW/125 kV = 4 kA; the current is four times higher to yield the same amount of power, because the voltage is four times less. The power lost in the transmission line is then PLOSS = (4 kA)2 ∗ 25 Ω = 400 MW = 80 percent of the power being transmitted. In general, line losses are inversely proportional to the square of the sending voltage; this is true for AC lines as well as DC. For this reason, historically power systems have sought to increase their transmission voltages as distances and amounts of power transmitted have grown. The highest common AC transmission voltages, sometimes referred to as extra high voltage (EHV), are 380 kV in Europe and 765 kV in the US. Voltages as high as 1200 kV have been used in Russia for some long-distance lines across Siberia. Above 1000 kV, however, the practical difficulty and expense of equipment and insulation that can withstand such high voltages becomes prohibitive. | ||
| Line 102: | Line 104: | ||
<br/> | <br/> | ||
| − | == Impedance, Reactance, Inductance, Capacitance == | + | === Impedance, Reactance, Inductance, Capacitance === |
AC circuits involve not only resistance but other physical phenomena that impede the flow of current. These are inductance and capacitance, referred to collectively as reactance. When AC currents pass through a reac tance (e.g. in transmission and distribution lines, in transformers, or in end-use equipment such as electric motors) some of the energy is temporarily stored in electro-magnetic fields. | AC circuits involve not only resistance but other physical phenomena that impede the flow of current. These are inductance and capacitance, referred to collectively as reactance. When AC currents pass through a reac tance (e.g. in transmission and distribution lines, in transformers, or in end-use equipment such as electric motors) some of the energy is temporarily stored in electro-magnetic fields. | ||
<u>This has three important implications:</u> | <u>This has three important implications:</u> | ||
| + | |||
#Even though energy is not “lost” to the environment as in the case of resistive heating, it must still be supplied to the reactive elements. This is known as reactive power. | #Even though energy is not “lost” to the environment as in the case of resistive heating, it must still be supplied to the reactive elements. This is known as reactive power. | ||
#Voltage decreases when current flows across a reactance, just as it does across a resistance. For AC circuits, Ohm’s Law must be modified: V = I∗Z, where Z is the sum of resistance and reactance, called impedance, and is measured in ohms. | #Voltage decreases when current flows across a reactance, just as it does across a resistance. For AC circuits, Ohm’s Law must be modified: V = I∗Z, where Z is the sum of resistance and reactance, called impedance, and is measured in ohms. | ||
| Line 117: | Line 120: | ||
<br/> | <br/> | ||
| − | == Complex Power: Real, Reactive, Apparent == | + | === Complex Power: Real, Reactive, Apparent === |
For AC systems, there are three kinds of power: real, reactive, and apparent. Real power (sometimes called active power) is what is consumed by resistances, and is measured in W (or kW, or MW). Reactive power is consumed by reactances, and is measured in volt-amperes reactive, or VAR (sometimes kVAR, or MVAR). Apparent power is the complex sum of real and reactive power, and is measured in voltamperes, or VA (or kVA or MVA). S = √(P2 + Q2), where S is apparent power, P is real power, and Q is reactive power. Apparent power is what must be supplied by the generators in a power system to meet the system’s electrical load, whereas end-use is generally measured in terms of real power only. Utilities always seek to minimize reactive power consumption, among other reasons because it is difficult to measure and be compensated for reactive power by customers. | For AC systems, there are three kinds of power: real, reactive, and apparent. Real power (sometimes called active power) is what is consumed by resistances, and is measured in W (or kW, or MW). Reactive power is consumed by reactances, and is measured in volt-amperes reactive, or VAR (sometimes kVAR, or MVAR). Apparent power is the complex sum of real and reactive power, and is measured in voltamperes, or VA (or kVA or MVA). S = √(P2 + Q2), where S is apparent power, P is real power, and Q is reactive power. Apparent power is what must be supplied by the generators in a power system to meet the system’s electrical load, whereas end-use is generally measured in terms of real power only. Utilities always seek to minimize reactive power consumption, among other reasons because it is difficult to measure and be compensated for reactive power by customers. | ||
| Line 123: | Line 126: | ||
<br/> | <br/> | ||
| − | == Loads and Power Factors | + | === Loads and Power Factors === |
An electrical load is the power drawn by an end-use device or customer connected to the power system. (Sometimes, “load” is used to refer to the end-use devices or customers themselves, but among engineers it usually refers to the power demand.) Loads can be resistive or reactive, and are often a combination of both. The extent to which a load is resistive is measured by its power factor, (p.f.), which is equal to the cosine of the phase difference between the current and voltage through the load: p.f. = cos φ. When the power factor is at its maximum value of one, the load is purely resistive. On the other hand, the smaller the power factor, the greater the phase difference and the greater the reactive power component of the load. Inductive loads, such as electric motors, have a lagging power factor (see 2.1.9), and are said to consume reactive power. Capacitive loads have a leading power factor and are said to be sources of reactive power. Given the voltages and currents through a circuit element, apparent, real, and reactive power can be calculated respectively as follows: S = IRMS * VRMS P = S * p.f. = IRMS * VRMS * cos φ Q = IRMS * VRMS * sin φ | An electrical load is the power drawn by an end-use device or customer connected to the power system. (Sometimes, “load” is used to refer to the end-use devices or customers themselves, but among engineers it usually refers to the power demand.) Loads can be resistive or reactive, and are often a combination of both. The extent to which a load is resistive is measured by its power factor, (p.f.), which is equal to the cosine of the phase difference between the current and voltage through the load: p.f. = cos φ. When the power factor is at its maximum value of one, the load is purely resistive. On the other hand, the smaller the power factor, the greater the phase difference and the greater the reactive power component of the load. Inductive loads, such as electric motors, have a lagging power factor (see 2.1.9), and are said to consume reactive power. Capacitive loads have a leading power factor and are said to be sources of reactive power. Given the voltages and currents through a circuit element, apparent, real, and reactive power can be calculated respectively as follows: S = IRMS * VRMS P = S * p.f. = IRMS * VRMS * cos φ Q = IRMS * VRMS * sin φ | ||
| − | Reactive loads can have a large effect on line losses, because the current flowing through a line, and the associated heating, is a function of the apparent power S rather than the real power P. For example, consider a load of 150 kW with a lagging power factor of 0.75, which is supplied by a 10 kV distribution line with a resistance of 10 Ω. The apparent power drawn by the load is S = P/p.f. = 150 kW/0.75 = 200 kVA. The current to the load is then I = 200 kVA/10 kV = 20 A. The line loss is PLOSS = I2 * R = (20 A)2 * 10 Ω = 4 kW. If there were no reactive power consumption by the load, the power factor would be equal to one. In that case, S = P = 150 kW. Then I = 150 kW/10 kV = 15 A, and PLOSS = (15 A)2 * 10 Ω = 2.25 kW. Thus the reactive load in this example increased the line losses from 2.25 kW to 4 kW, an increase of 78 %. | + | Reactive loads can have a large effect on line losses, because the current flowing through a line, and the associated heating, is a function of the apparent power S rather than the real power P. For example, consider a load of 150 kW with a lagging power factor of 0.75, which is supplied by a 10 kV distribution line with a resistance of 10 Ω. The apparent power drawn by the load is S = P/p.f. = 150 kW/0.75 = 200 kVA. The current to the load is then I = 200 kVA/10 kV = 20 A. The line loss is PLOSS = I2 * R = (20 A)2 * 10 Ω = 4 kW. If there were no reactive power consumption by the load, the power factor would be equal to one. In that case, S = P = 150 kW. Then I = 150 kW/10 kV = 15 A, and PLOSS = (15 A)2 * 10 Ω = 2.25 kW. Thus the reactive load in this example increased the line losses from 2.25 kW to 4 kW, an increase of 78 %. |
<br/> | <br/> | ||
| − | == Three-Phase Systems == | + | === Three-Phase Systems === |
House current is generally single-phase AC power, but the rest of the power system from generation to secondary distribution employs 3-phase AC. This means that transmission lines have three separate conductors, each carrying one-third of the power. The waveforms of the voltage in each phase are separated by 120°. | House current is generally single-phase AC power, but the rest of the power system from generation to secondary distribution employs 3-phase AC. This means that transmission lines have three separate conductors, each carrying one-third of the power. The waveforms of the voltage in each phase are separated by 120°. | ||
<u>There are two major reasons that 3-phase power became dominant</u>: | <u>There are two major reasons that 3-phase power became dominant</u>: | ||
| + | |||
#As long as the electrical loads on each phase are kept roughly balanced, only three wires are required to transmit power. Normally, any electric circuit requires both an “outbound” and “return” wire to make a complete circuit. Balanced 3-phase circuits provide their own return, and thus only three, rather than six, wires are required to transmit the same amount of power as three comparable single-phase systems. | #As long as the electrical loads on each phase are kept roughly balanced, only three wires are required to transmit power. Normally, any electric circuit requires both an “outbound” and “return” wire to make a complete circuit. Balanced 3-phase circuits provide their own return, and thus only three, rather than six, wires are required to transmit the same amount of power as three comparable single-phase systems. | ||
#Since the invention of polyphase induction motors by Nikola Tesla in the 1890s, 3-phase motors have been the workhorse of industry. More than one phase is required to balance torque, which increases the effectiveness and lifetime of both motors and generators. | #Since the invention of polyphase induction motors by Nikola Tesla in the 1890s, 3-phase motors have been the workhorse of industry. More than one phase is required to balance torque, which increases the effectiveness and lifetime of both motors and generators. | ||
| Line 145: | Line 149: | ||
<br/> | <br/> | ||
| − | == Basic Design Features | + | === Basic Design Features === |
<u>The basic design features of an interconnection include the following elements:</u> | <u>The basic design features of an interconnection include the following elements:</u> | ||
| + | |||
*whether it is AC or DC • if DC, whether it is single-pole or double-pole (+/-) | *whether it is AC or DC • if DC, whether it is single-pole or double-pole (+/-) | ||
*transmission capacity (in MVA) | *transmission capacity (in MVA) | ||
| Line 157: | Line 162: | ||
<u>These features are dictated by the answers to the following questions:</u> | <u>These features are dictated by the answers to the following questions:</u> | ||
| + | |||
*Will the interconnected systems operate synchronously or asynchronously? To operate synchronously, at a minimum the systems must have the same nominal frequency (50 Hz or 60 Hz). Even if frequencies are the same, technical and operational differences can make synchronous operation too difficult or expensive to pursue. Many synchronous networks with the same nominal frequency, including the four North American interconnections, have only asynchronous DC connections between them. | *Will the interconnected systems operate synchronously or asynchronously? To operate synchronously, at a minimum the systems must have the same nominal frequency (50 Hz or 60 Hz). Even if frequencies are the same, technical and operational differences can make synchronous operation too difficult or expensive to pursue. Many synchronous networks with the same nominal frequency, including the four North American interconnections, have only asynchronous DC connections between them. | ||
*What are the magnitudes and directions of the anticipated power flows? The basic rationales for the interconnection must be expressed quantitatively, using models that forecast the power flows through the interconnection among constituent systems. The forecasts must be conducted on different time scales: diurnal, seasonal, annual, and multi-year projections. | *What are the magnitudes and directions of the anticipated power flows? The basic rationales for the interconnection must be expressed quantitatively, using models that forecast the power flows through the interconnection among constituent systems. The forecasts must be conducted on different time scales: diurnal, seasonal, annual, and multi-year projections. | ||
| Line 164: | Line 170: | ||
<br/> | <br/> | ||
| − | == Interconnection Elements | + | === Interconnection Elements === |
A listing of the basic elements of an interconnection is provided below. Technical Objectives The ultimate objective of an interconnection, like the power systems it is part of, is to provide power to customers economically, safely, reliably, efficiently, and with minimal environmental impact. Each of these aspects has one or more quantitative measure, such as price per kilowatt-hour, number and lethality of accidents, frequency and duration of service interruptions, generating plant heat rate, transmission and distribution losses, and emissions factors. Interconnections are designed, and their individual components selected, with all of these objectives in mind, though they may be optimized differently in different systems. | A listing of the basic elements of an interconnection is provided below. Technical Objectives The ultimate objective of an interconnection, like the power systems it is part of, is to provide power to customers economically, safely, reliably, efficiently, and with minimal environmental impact. Each of these aspects has one or more quantitative measure, such as price per kilowatt-hour, number and lethality of accidents, frequency and duration of service interruptions, generating plant heat rate, transmission and distribution losses, and emissions factors. Interconnections are designed, and their individual components selected, with all of these objectives in mind, though they may be optimized differently in different systems. | ||
| Line 170: | Line 176: | ||
<br/> | <br/> | ||
| − | == Transmission Lines == | + | === Transmission Lines === |
Transmission lines come in two basic varieties: overhead lines and underground (or undersea) cables. Overhead lines are more common and generally less expensive than cables. The main design consideration for overhead lines is the choice of conductor type and size, which must balance the need to minimize impedance (and the associated losses), minimize cost, and minimize the weight that must be carried by support structures. Although copper is a better conductor, it has been overtaken in recent years by aluminum, which is lighter, cheaper, and in abundant supply. The most common variety of overhead conductor for high-capacity, long-distance transmission is stranded aluminum wire reinforced with steel (known as ACSR, for “aluminum conductor steel reinforced”). Other design considerations for overhead lines are the type of support structures (such as transmission towers and insulators) used, and the configuration of conductors on the support structures, which affects the reactance of the conductors and the strength of '''electromagnetic fields (EMFs)''' around the lines. Underground cables are used where overhead conductors are inappropriate due to environmental or land use considerations, such as in high-density urban areas or ecologically sensitive areas. Cables are insulated and are typically routed through underground conduits, and often require cooling systems to dissipate heat. Cables may use copper instead of aluminum, balancing the greater cost of copper against its superior conductivity and lower resistive heating. Undersea cables are usually made of copper, and may be surrounded by oil or an oil-soaked medium, then encased in insulating material to protect from corrosion. Undersea cables often have a coaxial structure, which has an inherently high capacitive reactance; therefore undersea cables are usually DC, which is not affected by reactance. Conductor cross-sections are typically measured in '''square centimeters (cm<sup>2</sup>) '''in the metric system, or thousands of '''circular mils (kcmil)''' in the American system (1 kcmil = 0.005 cm<sup>2</sup>). The capacity of a conductor to carry current without exceeding thermal limits is called its ampacity, measured in kA for large conductors.<br/> | Transmission lines come in two basic varieties: overhead lines and underground (or undersea) cables. Overhead lines are more common and generally less expensive than cables. The main design consideration for overhead lines is the choice of conductor type and size, which must balance the need to minimize impedance (and the associated losses), minimize cost, and minimize the weight that must be carried by support structures. Although copper is a better conductor, it has been overtaken in recent years by aluminum, which is lighter, cheaper, and in abundant supply. The most common variety of overhead conductor for high-capacity, long-distance transmission is stranded aluminum wire reinforced with steel (known as ACSR, for “aluminum conductor steel reinforced”). Other design considerations for overhead lines are the type of support structures (such as transmission towers and insulators) used, and the configuration of conductors on the support structures, which affects the reactance of the conductors and the strength of '''electromagnetic fields (EMFs)''' around the lines. Underground cables are used where overhead conductors are inappropriate due to environmental or land use considerations, such as in high-density urban areas or ecologically sensitive areas. Cables are insulated and are typically routed through underground conduits, and often require cooling systems to dissipate heat. Cables may use copper instead of aluminum, balancing the greater cost of copper against its superior conductivity and lower resistive heating. Undersea cables are usually made of copper, and may be surrounded by oil or an oil-soaked medium, then encased in insulating material to protect from corrosion. Undersea cables often have a coaxial structure, which has an inherently high capacitive reactance; therefore undersea cables are usually DC, which is not affected by reactance. Conductor cross-sections are typically measured in '''square centimeters (cm<sup>2</sup>) '''in the metric system, or thousands of '''circular mils (kcmil)''' in the American system (1 kcmil = 0.005 cm<sup>2</sup>). The capacity of a conductor to carry current without exceeding thermal limits is called its ampacity, measured in kA for large conductors.<br/> | ||
| Line 176: | Line 182: | ||
<br/> | <br/> | ||
| − | == Support Structures == | + | === Support Structures === |
There are many possible types of support structures for overhead transmission lines. In developed countries, transmission lines are supported on structures made out of steel lattice, tubular steel, wood, and concrete. Of these, steel lattice has the highest strength to weight ratio, and is the easiest to assemble in areas that are difficult to access<ref name="John Reason, “Special Report: Transmission Structures,”Electrical World, 206, 3 (March 992), pp. 3-49">John Reason, “Special Report: Transmission Structures,”Electrical World, 206, 3 (March 992), pp. 3-49</ref>. Where aesthetics are an important factor, however, other materials are often used. The main function of support structures is to keep the conductors from contacting trees or other objects, including people and animals; thus the structures must be tall enough to do so even when the conductors sag due to high temperatures caused by resistive heating.<br/> | There are many possible types of support structures for overhead transmission lines. In developed countries, transmission lines are supported on structures made out of steel lattice, tubular steel, wood, and concrete. Of these, steel lattice has the highest strength to weight ratio, and is the easiest to assemble in areas that are difficult to access<ref name="John Reason, “Special Report: Transmission Structures,”Electrical World, 206, 3 (March 992), pp. 3-49">John Reason, “Special Report: Transmission Structures,”Electrical World, 206, 3 (March 992), pp. 3-49</ref>. Where aesthetics are an important factor, however, other materials are often used. The main function of support structures is to keep the conductors from contacting trees or other objects, including people and animals; thus the structures must be tall enough to do so even when the conductors sag due to high temperatures caused by resistive heating.<br/> | ||
| Line 182: | Line 188: | ||
All things being equal, taller structures also minimize ground-level EMFs. Because overhead transmission lines are not insulated, they are typically suspended from towers on strings of ceramic insulators, which are designed to prevent flashover, or the leakage of current from the conductors to the tower, which would present a lethal prospect to anyone touching the tower. AC transmission towers are usually designed to carry three conductors: the three phases of AC power systems. Towers that hold these in an equilateral triangle shape (called a “delta”) keep the mutual reactances of the three phases balanced; non-delta configurations often require that conductors be transposed, or switch places, at regular intervals along the transmission path. Some towers carry more than one circuit, with three phases per circuit; for example, a double-circuit tower will have six conductors. (The conductor for each phase may also be subdivided into “bundles” of two or more conductors, which are physically close together.) DC transmission towers carry two conductors per circuit. Figure 2-1 on the following page shows various options for transmission tower design. | All things being equal, taller structures also minimize ground-level EMFs. Because overhead transmission lines are not insulated, they are typically suspended from towers on strings of ceramic insulators, which are designed to prevent flashover, or the leakage of current from the conductors to the tower, which would present a lethal prospect to anyone touching the tower. AC transmission towers are usually designed to carry three conductors: the three phases of AC power systems. Towers that hold these in an equilateral triangle shape (called a “delta”) keep the mutual reactances of the three phases balanced; non-delta configurations often require that conductors be transposed, or switch places, at regular intervals along the transmission path. Some towers carry more than one circuit, with three phases per circuit; for example, a double-circuit tower will have six conductors. (The conductor for each phase may also be subdivided into “bundles” of two or more conductors, which are physically close together.) DC transmission towers carry two conductors per circuit. Figure 2-1 on the following page shows various options for transmission tower design. | ||
| − | |||
| − | == Transformers and Substations == | + | === Transformers and Substations === |
Transformers are used to change voltage levels in AC circuits, allowing transmission at high voltages to minimize resistive losses, and low voltages at the customer end for safety. This ability, following the development of transformers by William Stanley in 1885, led to the rapid adoption of AC systems over DC systems. The essential element of a transformer consists of two coils of wire wrapped around an iron core. An alternating current in one coil produces a changing electromagnetic field that induces a current in the other. The voltages on either side are in the same ratio as the number of turns on each coil. For example, a transformer with a 10:1 “turns ratio” that is connected to a 15 kV supply on its primary side, will have a voltage of 150 kV on its secondary side. Transformers step up the voltage from generator to transmission system, and other transformers step it down, often in several stages, from transmission to sub-transmission to primary distribution to secondary distribution, and finally to the end-user voltage, such as 120 V. At the distribution level, transformers often have taps that can be used to change the turns ratio; this allows operators to maintain customer voltage levels when system voltages change. Modern transformers are extremely efficient, typically greater than 99%, but even small losses can produce a great deal of heat, which must be dissipated to prevent damage to the equipment. Large transformers are cooled by circulating oil, which also functions as an electrical insulator. | Transformers are used to change voltage levels in AC circuits, allowing transmission at high voltages to minimize resistive losses, and low voltages at the customer end for safety. This ability, following the development of transformers by William Stanley in 1885, led to the rapid adoption of AC systems over DC systems. The essential element of a transformer consists of two coils of wire wrapped around an iron core. An alternating current in one coil produces a changing electromagnetic field that induces a current in the other. The voltages on either side are in the same ratio as the number of turns on each coil. For example, a transformer with a 10:1 “turns ratio” that is connected to a 15 kV supply on its primary side, will have a voltage of 150 kV on its secondary side. Transformers step up the voltage from generator to transmission system, and other transformers step it down, often in several stages, from transmission to sub-transmission to primary distribution to secondary distribution, and finally to the end-user voltage, such as 120 V. At the distribution level, transformers often have taps that can be used to change the turns ratio; this allows operators to maintain customer voltage levels when system voltages change. Modern transformers are extremely efficient, typically greater than 99%, but even small losses can produce a great deal of heat, which must be dissipated to prevent damage to the equipment. Large transformers are cooled by circulating oil, which also functions as an electrical insulator. | ||
| − | [[File:Towers.jpg|thumb|right|300px|From Chapter 4 of US Nuclear Regulatory Commission (NRC,996), Generic Environmental Impact Statement for License Renewal of Nuclear Plants (Report # NUREG- 437 Vol. ), | + | [[File:Towers.jpg|thumb|right|300px|From Chapter 4 of US Nuclear Regulatory Commission (NRC,996), Generic Environmental Impact Statement for License Renewal of Nuclear Plants (Report # NUREG- 437 Vol. ), Original source: R. L. Kroodsma and J. W. Van Dyke (985),Technical and Environmental Aspects of Electric Power Transmission, Report # ORNL-6 65, Oak Ridge National Laboratory, Oak Ridge, Tennessee]] |
Large transformers are housed in substations, where sections of a transmission and distribution system operating at different voltages are joined. Larger substations have a manned control room, while smaller substations often operate automatically. In addition to transformers, important substation equipment includes switchgear, circuit breakers and other protective equipment (see next section), and capacitor banks used to provide reactive power support. | Large transformers are housed in substations, where sections of a transmission and distribution system operating at different voltages are joined. Larger substations have a manned control room, while smaller substations often operate automatically. In addition to transformers, important substation equipment includes switchgear, circuit breakers and other protective equipment (see next section), and capacitor banks used to provide reactive power support. | ||
| + | |||
<br/> | <br/> | ||
| − | == Protection Systems == | + | === Protection Systems === |
| − | Protection systems are an extremely important part of any power system. Their primary function is to detect and clear faults, which are inadvertent electrical connections – that is, short circuits – between system components at different voltages. When faults occur, very high currents can result, typically 2-10 times as high as normal load currents. Since power is proportional to I2, a great deal of energy can be delivered to unintended recipients in a very short time. The goal of protection systems is to isolate and de-energize faults before they can harm personnel or cause serious damage to equipment. Note that protection systems are designed to protect the power system itself, rather than end-user equipment. The key components of protection systems are circuit breakers, instrument transformers, and relays. Circuit breakers are designed to interrupt a circuit in which high levels of current are flowing, typically within three voltage cycles (about 50 milliseconds in a 60 Hz system). <br/> | + | Protection systems are an extremely important part of any power system. Their primary function is to detect and clear faults, which are inadvertent electrical connections – that is, short circuits – between system components at different voltages. When faults occur, very high currents can result, typically 2-10 times as high as normal load currents. Since power is proportional to I2, a great deal of energy can be delivered to unintended recipients in a very short time. The goal of protection systems is to isolate and de-energize faults before they can harm personnel or cause serious damage to equipment. Note that protection systems are designed to protect the power system itself, rather than end-user equipment. The key components of protection systems are circuit breakers, instrument transformers, and relays. Circuit breakers are designed to interrupt a circuit in which high levels of current are flowing, typically within three voltage cycles (about 50 milliseconds in a 60 Hz system).<br/> |
To do this they must quench the electric arc that appears when the breaker contacts are opened; this is usually accomplished by blowing a gas, such as compressed air or sulfur hexafluoride (SF6) across the contacts. Since human operators generally could not respond to a fault in time to prevent damage, circuit breakers are operated by automatic relays that sense faults or other undesirable system conditions. To distinguish between normal operations and fault conditions, relays are connected to instrument transformers – '''voltage transformers (VT)''' and '''current transformers (CT)''' – that reflect the voltages and currents of the equipment they are connected to. Relays themselves can be either electromechanical or solid state devices. Essential aspects of protection system design include determining the specifications and placement of protection equipment, and also the correct timing and sequence of relay operations. Protection engineers must determine how long an undesirable condition should be allowed to persist before opening a circuit breaker, and the order in which circuit breakers must open to correctly isolate faults in different zones<ref name="J. Blackburn (998), Protective Relaying: Principles and Applications , 2nd ed. Marcel Dekker, New York.">J. Blackburn (998), Protective Relaying: Principles and Applications , 2nd ed. Marcel Dekker, New York.</ref>.<br/> | To do this they must quench the electric arc that appears when the breaker contacts are opened; this is usually accomplished by blowing a gas, such as compressed air or sulfur hexafluoride (SF6) across the contacts. Since human operators generally could not respond to a fault in time to prevent damage, circuit breakers are operated by automatic relays that sense faults or other undesirable system conditions. To distinguish between normal operations and fault conditions, relays are connected to instrument transformers – '''voltage transformers (VT)''' and '''current transformers (CT)''' – that reflect the voltages and currents of the equipment they are connected to. Relays themselves can be either electromechanical or solid state devices. Essential aspects of protection system design include determining the specifications and placement of protection equipment, and also the correct timing and sequence of relay operations. Protection engineers must determine how long an undesirable condition should be allowed to persist before opening a circuit breaker, and the order in which circuit breakers must open to correctly isolate faults in different zones<ref name="J. Blackburn (998), Protective Relaying: Principles and Applications , 2nd ed. Marcel Dekker, New York.">J. Blackburn (998), Protective Relaying: Principles and Applications , 2nd ed. Marcel Dekker, New York.</ref>.<br/> | ||
| − | + | === Communications, Monitoring, and Control Systems === | |
| − | |||
| − | == Communications, Monitoring, and Control Systems == | ||
Power system operations take place within geographically well-defined control areas, which traditionally corresponded to a utility’s service territory. With market liberalization, individual utility control areas have sometimes been combined into larger control areas under the jurisdiction of an '''independent system operator (ISO)'''. In either case, system operations are coordinated by a central control center, the responsibility of which it is to keep the entire system running safely and reliably. This entails continuously monitoring system conditions and deploying system resources as the situation requires. Traditionally, monitoring and control have been conducted semi-manually, with a heavy reliance on telephone communications with plant operators and field personnel.<br/> | Power system operations take place within geographically well-defined control areas, which traditionally corresponded to a utility’s service territory. With market liberalization, individual utility control areas have sometimes been combined into larger control areas under the jurisdiction of an '''independent system operator (ISO)'''. In either case, system operations are coordinated by a central control center, the responsibility of which it is to keep the entire system running safely and reliably. This entails continuously monitoring system conditions and deploying system resources as the situation requires. Traditionally, monitoring and control have been conducted semi-manually, with a heavy reliance on telephone communications with plant operators and field personnel.<br/> | ||
| Line 210: | Line 214: | ||
<br/> | <br/> | ||
| − | = Technical Issues Associated with AC Grid Interconnection | + | == Technical Issues Associated with AC Grid Interconnection == |
| − | == General Requirements for AC Interconnection | + | === General Requirements for AC Interconnection === |
AC interconnection usually provides the greatest interconnection benefits, except in certain cases for which DC is the preferred option (see Section 2.4.1). Synchronous interconnection of different systems is, however, technically demanding. At a general level, the first requirement is that the systems share the same nominal frequency, either 50 Hz or 60 Hz. Then, they must regulate frequency so that they achieve and remain in synchronism (see Section 2.3.4, below). They must also interconnect at a common voltage level. This is easier if the countries involved have agreed to a common standard for transmission voltage, such as the 380 kV standard in Europe.<br/> | AC interconnection usually provides the greatest interconnection benefits, except in certain cases for which DC is the preferred option (see Section 2.4.1). Synchronous interconnection of different systems is, however, technically demanding. At a general level, the first requirement is that the systems share the same nominal frequency, either 50 Hz or 60 Hz. Then, they must regulate frequency so that they achieve and remain in synchronism (see Section 2.3.4, below). They must also interconnect at a common voltage level. This is easier if the countries involved have agreed to a common standard for transmission voltage, such as the 380 kV standard in Europe.<br/> | ||
| Line 220: | Line 224: | ||
<br/> | <br/> | ||
| − | == Technical Issues for AC Interconnection<br/> | + | === Technical Issues for AC Interconnection === |
| + | |||
| + | One way of thinking about the technical issues of AC interconnections is to group them into those associated with the transmission interconnection itself, and those associated with operating the larger interconnected system. Transmission issues are discussed in <span style="color:#008000">[[Technical Aspects of Grid Interconnection#Transmission Issues|Key issues include thermal limits]], </span>stability limits, and voltage regulation, which are the main constraints on transmission line operation. Other transmission issues include loop and parallel path flows, available transfer capacity, and FACTS technologies. System-wide issues are discussed in [http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,_page_16 including frequency regulation,]<span style="color:#008000">p</span>ower quality, the coordination of planning and operations, political and institutional cooperation, systems that are aging or in poor repair, and the operation of nuclear power plants. The implications of electricity market liberalization for interconnected systems are also discussed. | ||
| + | |||
| + | <br/> | ||
| − | + | === Transmission Issues === | |
| − | + | '''Thermal limits''' | |
| − | + | The capacity of transmission lines, transformers, and other equipment is determined by temperature limits. If these limits are exceeded, the equipment can be damaged or destroyed. Equipment ratings have traditionally been conservative, and operators have stayed well below the rated limits, but increased power trading in liberalized markets has created pressure for higher utilization. Instead of a single thermal limit, dynamic ratings are now often used. For example, transmission lines can carry more current when heat is effectively dissipated, and thus will have a higher rating on cold, windy days without direct sunlight. When transmission lines heat up, the metal expands and the line sags. If the sag becomes too great, lines can come into contact with surrounding objects, causing a fault. Excess sag can also cause the metal to lose tensile strength due to annealing, after which it will not shrink back to its original length. Important transmission lines are often monitored by a device called a “sagometer”, which measures the amount of sag, making system operators aware of dangerous sag conditions. | |
| − | + | <br/> | |
| − | Stability limits<br/> | + | '''Stability limits'''<br/> |
The stability limit of a transmission line is the maximum amount of power that can be transmitted for which the system will remain synchronized if a disturbance occurs. The power flow through a transmission line is governed by the difference in power angle between the sending and receiving sides: P = VR ∗ VS ∗ sinδ / X | The stability limit of a transmission line is the maximum amount of power that can be transmitted for which the system will remain synchronized if a disturbance occurs. The power flow through a transmission line is governed by the difference in power angle between the sending and receiving sides: P = VR ∗ VS ∗ sinδ / X | ||
| Line 238: | Line 246: | ||
<br/> | <br/> | ||
| − | == Voltage Regulation == | + | === Voltage Regulation === |
Utilities generally maintain system voltages within 5-10 percent of nominal values in order to avoid the risk of voltage collapse, which can lead to a major interruption of service. Power system voltages are primarily governed by reactive power flows. Voltages along a transmission link are a function of the physical length of the circuit, the impedance per unit length, and the flow of real power: the higher the current and the greater the reactance, the larger the voltage drop (if the reactance is predominantly inductive) or gain (if capacitive). Voltage collapse can be triggered when reactive demand is high and systems are operating near their stability limits, then undergo a disturbance that triggers a quick downward spiral. To maintain voltages along long AC transmission lines, reactive compensation of various kinds can be employed, such as series and shunt capacitors, and shunt reactors. (See section on FACTS, below). System operators also maintain voltage levels in order to protect end-use equipment (for example, low voltages cause motor currents to increase, and higher currents can cause thermal damage). Utilities are usually obliged to provide power to customers within prescribed voltage tolerances. Devices called tap-changing transformers in the local distribution system are used to ensure that customer voltages are maintained even when system voltages change substantially. Note, however, that the power quality experienced by the customer is generally more affected by local conditions in the distribution system, such as switching, lightning strikes, and the loads of other customers, than by conditions in the transmission system. Protecting sensitive electronic end-use equipment is the responsibility of the customer rather than the utility. | Utilities generally maintain system voltages within 5-10 percent of nominal values in order to avoid the risk of voltage collapse, which can lead to a major interruption of service. Power system voltages are primarily governed by reactive power flows. Voltages along a transmission link are a function of the physical length of the circuit, the impedance per unit length, and the flow of real power: the higher the current and the greater the reactance, the larger the voltage drop (if the reactance is predominantly inductive) or gain (if capacitive). Voltage collapse can be triggered when reactive demand is high and systems are operating near their stability limits, then undergo a disturbance that triggers a quick downward spiral. To maintain voltages along long AC transmission lines, reactive compensation of various kinds can be employed, such as series and shunt capacitors, and shunt reactors. (See section on FACTS, below). System operators also maintain voltage levels in order to protect end-use equipment (for example, low voltages cause motor currents to increase, and higher currents can cause thermal damage). Utilities are usually obliged to provide power to customers within prescribed voltage tolerances. Devices called tap-changing transformers in the local distribution system are used to ensure that customer voltages are maintained even when system voltages change substantially. Note, however, that the power quality experienced by the customer is generally more affected by local conditions in the distribution system, such as switching, lightning strikes, and the loads of other customers, than by conditions in the transmission system. Protecting sensitive electronic end-use equipment is the responsibility of the customer rather than the utility. | ||
| Line 244: | Line 252: | ||
<br/> | <br/> | ||
| − | == Loop and Parallel Path Flows | + | === Loop and Parallel Path Flows === |
In power systems, power flows do not necessarily follow a specified transmission path – for example, from seller in system A to buyer in system B - but divide themselves among various connected transmission paths according to the voltage levels and impedances of the path. To put it another way, power flows conform to physical laws rather than economic agreements. In some cases, a power transaction can take quite unwanted paths, resulting in line losses and possibly overloading lines of neighbors having nothing to do economically with the transaction. In general, these phenomena are referred to as circulating power, loop flows, and parallel path flows. A well-known example of these flows is that in a power transfer from the U.S. Pacific Northwest to the state of Utah, one-third of the power flows through Southern California, and another one-third flows through Arizona.<ref>John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World, April 998, p.63</ref> What is important for the reliability of an interconnected system is that operators know the sources and destinations of all transactions and where the power will flow, and are able to calculate the resulting reliability risks (see section on power flow modeling, below). | In power systems, power flows do not necessarily follow a specified transmission path – for example, from seller in system A to buyer in system B - but divide themselves among various connected transmission paths according to the voltage levels and impedances of the path. To put it another way, power flows conform to physical laws rather than economic agreements. In some cases, a power transaction can take quite unwanted paths, resulting in line losses and possibly overloading lines of neighbors having nothing to do economically with the transaction. In general, these phenomena are referred to as circulating power, loop flows, and parallel path flows. A well-known example of these flows is that in a power transfer from the U.S. Pacific Northwest to the state of Utah, one-third of the power flows through Southern California, and another one-third flows through Arizona.<ref>John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World, April 998, p.63</ref> What is important for the reliability of an interconnected system is that operators know the sources and destinations of all transactions and where the power will flow, and are able to calculate the resulting reliability risks (see section on power flow modeling, below). | ||
| Line 250: | Line 258: | ||
<br/> | <br/> | ||
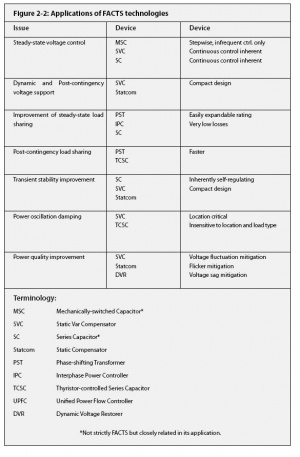
| − | == Available Transmission Capacity (ATC) == | + | === Available Transmission Capacity (ATC) === |
An important measure of transmission capacity is '''transmission transfer capability (TTC)''', which is the maximum power flow that a line can accommodate at any given time and still be able to survive the loss of a major generator or transmission link elsewhere in the system. '''Available transmission capacity (ATC)''' is the TTC of a line minus the amount of capacity already committed to other uses on that line. ATC is thus the measure of how much power can be safely transmitted over a transmission line at a given time while ensuring overall system reliability. | An important measure of transmission capacity is '''transmission transfer capability (TTC)''', which is the maximum power flow that a line can accommodate at any given time and still be able to survive the loss of a major generator or transmission link elsewhere in the system. '''Available transmission capacity (ATC)''' is the TTC of a line minus the amount of capacity already committed to other uses on that line. ATC is thus the measure of how much power can be safely transmitted over a transmission line at a given time while ensuring overall system reliability. | ||
| Line 256: | Line 264: | ||
<br/> | <br/> | ||
| − | == Flexible AC Transmission System (FACTS) | + | === Flexible AC Transmission System (FACTS) === |
'''Flexible AC Transmission System (FACTS)''' refers to a number of different technologies based on power electronics and advanced control technologies, which are used to optimize power flows and increase grid stability<ref>A. Edris (2000), “FACTS Technology Development: An Update,”fckLRIEEE Power Engineering Review, March 2000</ref>. FACTS equipment is expensive, but it can pay for itself by directing power flows with precision, eliminating loop flows, and relieving transmission bottlenecks without requiring that new lines be built. It can also improve frequency and voltage stability, decrease transmission losses and voltage drops, and improve power quality. FACTS equipment includes static compensators, static VAR compensators, thyristor-controlled series capacitors, phase-shifting transformers, interphase power controllers, universal power flow controllers, and dynamic voltage restorers. With FACTS, AC transmission over distances that were not previously possible due to stability limits has become possible. Figure 2-2 shows, on the following page, applications for different FACTS technologies. FACTS devices have been used extensively in the North American and European interconnections, and increasingly in developing regions, including the South Africa-Zimbabwe interconnection, the Brazil north-south interconnection, and other interconnections in Latin America, Africa, and South Asia. | '''Flexible AC Transmission System (FACTS)''' refers to a number of different technologies based on power electronics and advanced control technologies, which are used to optimize power flows and increase grid stability<ref>A. Edris (2000), “FACTS Technology Development: An Update,”fckLRIEEE Power Engineering Review, March 2000</ref>. FACTS equipment is expensive, but it can pay for itself by directing power flows with precision, eliminating loop flows, and relieving transmission bottlenecks without requiring that new lines be built. It can also improve frequency and voltage stability, decrease transmission losses and voltage drops, and improve power quality. FACTS equipment includes static compensators, static VAR compensators, thyristor-controlled series capacitors, phase-shifting transformers, interphase power controllers, universal power flow controllers, and dynamic voltage restorers. With FACTS, AC transmission over distances that were not previously possible due to stability limits has become possible. Figure 2-2 shows, on the following page, applications for different FACTS technologies. FACTS devices have been used extensively in the North American and European interconnections, and increasingly in developing regions, including the South Africa-Zimbabwe interconnection, the Brazil north-south interconnection, and other interconnections in Latin America, Africa, and South Asia. | ||
| Line 262: | Line 270: | ||
<br/> | <br/> | ||
| − | == Transmission Upgrades | + | === Transmission Upgrades === |
If existing transmission facilities are to be used in the interconnection but are not adequate to transmit the expected volume of power, they can be upgraded either by adding additional lines in parallel or increasing the transmission voltage. If these options are not available, FACTS or HVDC solutions can be explored. | If existing transmission facilities are to be used in the interconnection but are not adequate to transmit the expected volume of power, they can be upgraded either by adding additional lines in parallel or increasing the transmission voltage. If these options are not available, FACTS or HVDC solutions can be explored. | ||
| Line 268: | Line 276: | ||
<br/> | <br/> | ||
| − | == Systems Issues | + | === Systems Issues === |
Key technical systems issues that must be addressed in planning and implementing a grid interconnection include frequency regulation, coordination of operations, interconnections of power systems with weak grids, and aspects of interconnection that are associated with electricity market liberalization. Frequency Regulation Controlling frequency in a synchronous network is ultimately an issue of precisely matching generation to load. This load-matching occurs on several time scales. System planners and operators plan generation from hours to months in advance, coordinating the dispatch of generating units and power exchanges with other systems based on factors such as historical load patterns, weather predictions, maintenance | Key technical systems issues that must be addressed in planning and implementing a grid interconnection include frequency regulation, coordination of operations, interconnections of power systems with weak grids, and aspects of interconnection that are associated with electricity market liberalization. Frequency Regulation Controlling frequency in a synchronous network is ultimately an issue of precisely matching generation to load. This load-matching occurs on several time scales. System planners and operators plan generation from hours to months in advance, coordinating the dispatch of generating units and power exchanges with other systems based on factors such as historical load patterns, weather predictions, maintenance | ||
| Line 278: | Line 286: | ||
<br/> | <br/> | ||
| − | == Coordinating Operations == | + | === Coordinating Operations === |
The basic geographical unit of a power system is the control area, which typically has a single control center responsible for monitoring system conditions and scheduling the dispatch of all generation. In interconnected systems, transmission lines to neighboring control areas are metered and the incoming and outgoing power flows are scheduled and continuously monitored. A continuous record of the balance of load, generation, and exchanges with other control areas called the '''Area Control Error (ACE)''' is used to plan real-time corrections to maintain load-generation balance. Interconnections create a number of coordination challenges, both institutional and technical. For example, reliability standards and constraints may differ, and there may be differences in regulation and control schemes and technologies. It is important for the operators and planners of interconnected systems to be aware of the conditions and practices in their neighboring control areas. Good communication between different system operators is important for agreeing on and coordinating interchange schedules, transmission loading, maintenance schedules, procedures for fault clearing, and emergency protocols<ref>John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World , April 998, p.62</ref>. As interconnected systems expand to encompass large geographical scales, technology is striving to keep up with the associated complexities and risks.<br/> | The basic geographical unit of a power system is the control area, which typically has a single control center responsible for monitoring system conditions and scheduling the dispatch of all generation. In interconnected systems, transmission lines to neighboring control areas are metered and the incoming and outgoing power flows are scheduled and continuously monitored. A continuous record of the balance of load, generation, and exchanges with other control areas called the '''Area Control Error (ACE)''' is used to plan real-time corrections to maintain load-generation balance. Interconnections create a number of coordination challenges, both institutional and technical. For example, reliability standards and constraints may differ, and there may be differences in regulation and control schemes and technologies. It is important for the operators and planners of interconnected systems to be aware of the conditions and practices in their neighboring control areas. Good communication between different system operators is important for agreeing on and coordinating interchange schedules, transmission loading, maintenance schedules, procedures for fault clearing, and emergency protocols<ref>John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World , April 998, p.62</ref>. As interconnected systems expand to encompass large geographical scales, technology is striving to keep up with the associated complexities and risks.<br/> | ||
<u>Some important trends in grid technologies related to the problems of maintaining reliability in large AC systems include<ref>Karl Stahlkopf and Philip Sharp (998), “Reliability in Power Delivery: Where Technology and Politics Meet,”Public Utilities Fortnightly, January5,998</ref>:</u> | <u>Some important trends in grid technologies related to the problems of maintaining reliability in large AC systems include<ref>Karl Stahlkopf and Philip Sharp (998), “Reliability in Power Delivery: Where Technology and Politics Meet,”Public Utilities Fortnightly, January5,998</ref>:</u> | ||
| + | |||
#Faster physical control over the system, for example FACTS technologies with solid state controls that allow rapid adjustment of reactive power flows. | #Faster physical control over the system, for example FACTS technologies with solid state controls that allow rapid adjustment of reactive power flows. | ||
#Improved real-time monitoring ability, for example the development of wide area monitoring systems (WAMS). | #Improved real-time monitoring ability, for example the development of wide area monitoring systems (WAMS). | ||
| Line 290: | Line 299: | ||
<br/> | <br/> | ||
| − | == Interconnection of Power Systems with Weak Grids | + | == Interconnection of Power Systems with Weak Grids == |
Not all interconnections take place between power systems in top technical condition. In the developing world, many power systems bear the marks of age, poor repair, and insufficient investment, ranging from corroded conductors and deteriorating insulation to leaking transformers, worn out switchgear, and a variety of inoperable equipment. Equipment is often obsolete, and operations that are automated elsewhere may be carried out manually. Systems in poor repair generally perform poorly, have serious reliability problems, and often fail to comply with safety or environmental standards. <u>As one scholar described the difficulties of interconnection among sparse, poorly maintained systems:</u> | Not all interconnections take place between power systems in top technical condition. In the developing world, many power systems bear the marks of age, poor repair, and insufficient investment, ranging from corroded conductors and deteriorating insulation to leaking transformers, worn out switchgear, and a variety of inoperable equipment. Equipment is often obsolete, and operations that are automated elsewhere may be carried out manually. Systems in poor repair generally perform poorly, have serious reliability problems, and often fail to comply with safety or environmental standards. <u>As one scholar described the difficulties of interconnection among sparse, poorly maintained systems:</u> | ||
| Line 302: | Line 311: | ||
<br/> | <br/> | ||
| − | == Interconnections and Electricity Market Liberalization | + | == Interconnections and Electricity Market Liberalization == |
Electricity market liberalization presents a combination of opportunities, challenges, and risks for interconnection projects. From the economic standpoint, the opportunity of greater access to lower-cost supplies is balanced against the challenge of operating competitive markets and the risk of market breakdowns of the type that occurred in California in 2000-2001. From the technical standpoint, the focus is on the impact of liberalization on reliability<ref>George C. Loehr (998), “Ten Myths about Electric Deregulation”.fckLRPublic Utilities Fortnightly , April 15, 1998</ref>. | Electricity market liberalization presents a combination of opportunities, challenges, and risks for interconnection projects. From the economic standpoint, the opportunity of greater access to lower-cost supplies is balanced against the challenge of operating competitive markets and the risk of market breakdowns of the type that occurred in California in 2000-2001. From the technical standpoint, the focus is on the impact of liberalization on reliability<ref>George C. Loehr (998), “Ten Myths about Electric Deregulation”.fckLRPublic Utilities Fortnightly , April 15, 1998</ref>. | ||
<u>Some of the main concerns that have been raised include:</u> | <u>Some of the main concerns that have been raised include:</u> | ||
| + | |||
*Increased or excessive utilization of transmission capacity, reducing reliability margins | *Increased or excessive utilization of transmission capacity, reducing reliability margins | ||
*Reduced information exchange among system operators due to proprietary concerns in a competitive environment | *Reduced information exchange among system operators due to proprietary concerns in a competitive environment | ||
| Line 317: | Line 327: | ||
<u>Requirements for successful interconnection operation in a liberalized, more market-driven electricity sector environment include<ref>F. Meslier (1999), “Historical Background and Lessons for the Future,” in J. Casazza and G. Loehr, The Evolution of Electric Power Transmission Under Deregulation , IEEE, Piscataway, NJ; p.37</ref>:</u> | <u>Requirements for successful interconnection operation in a liberalized, more market-driven electricity sector environment include<ref>F. Meslier (1999), “Historical Background and Lessons for the Future,” in J. Casazza and G. Loehr, The Evolution of Electric Power Transmission Under Deregulation , IEEE, Piscataway, NJ; p.37</ref>:</u> | ||
| + | |||
*Make knowledge of all transactions available to system operators | *Make knowledge of all transactions available to system operators | ||
*Improve cooperation between network managers of different countries | *Improve cooperation between network managers of different countries | ||
*Improve incentives for investing in infrastructure | *Improve incentives for investing in infrastructure | ||
*Clearly define the rights and obligations of all parties | *Clearly define the rights and obligations of all parties | ||
| − | *Monitor behavior and rigorously enforce | + | *Monitor behavior and rigorously enforce rule |
| − | = | + | <br/> |
| + | |||
| + | <br/> | ||
| + | |||
| + | == Further Information == | ||
| + | |||
| + | *[[Portal:Grid|Grid Portal on energypedia]] | ||
| + | *[[Rural Electrification - Minimum Safety Standards for Household Connection|Rural Electrification - Minimum Safety Standards for Household Connection]] | ||
| + | *[[Permissible_Voltage_Drop|Permissible Voltage Drop]]<br/> | ||
| + | *[[Grid Interconnection of Micro-hydro Projects (MHPs) in Nepal|Grid Interconnection of Micro-hydro Projects (MHPs) in Nepal]] | ||
| + | |||
| + | <br/> | ||
| − | |||
| − | = References | + | == References == |
| − | This information is originally from the | + | This information is originally from the chapter [http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf Technical Aspects of Grid Interconnection], published in UN DESA (2006): Multi Dimensional Issues in International Electric Power Grid Interconnections.<br/> |
<references /><br/> | <references /><br/> | ||
[[Category:Grid]] | [[Category:Grid]] | ||
Latest revision as of 09:06, 6 November 2024
Overview - The Evolution of Interconnected Systems[1]
Electricity grid interconnections have played a key role in the history of electric power systems. Most national and regional power systems that exist today began many decades ago as isolated systems, often as a single generator in a large city. As power systems expanded out from their urban cores, interconnections among neighboring systems became increasingly common[2] . Groups of utilities began to form power pools, allowing them to trade electricity and share capacity reserves. The first power pool in the United States was formed in the Connecticut Valley in 1925[3].
As transmission technologies improved, long distance interconnections developed, sometimes crossing national borders. The first international interconnections in Europe came in 1906, when Switzerland built transmission links to France and Italy. One of the great engineering achievements of the last century has been the evolution of large synchronous alternating current (AC) power grids, in which all the interconnected systems maintain the same precise electrical frequency. Today, the North American power system is composed of four giant synchronous systems, namely the Eastern, Western, Texas, and Quebec interconnections.
The Eastern interconnection by itself has been called the largest machine in the world, consisting of thousands of generators, millions of kilometers of transmission and distribution lines, and more than a billion different electrical loads. Despite this complexity, the network operates in synchronism as a single system. So does the Western European interconnection, which reaches from the UK and Scandinavia to Italy and Greece, embracing along the way much of Eastern Europe (for example, Poland, Hungary, Slovakia, and the Czech Republic). Synchronous interconnections among countries are expanding in Central and South America, North and Sub-Saharan Africa, and the Middle East[4].
At the same time that synchronous AC networks have reached the continental scale, the use of high voltage direct current (HVDC) interconnections is also rapidly expanding as a result of technical progress over the last two decades. HVDC permits the asynchronous interconnection of networks that operate at different frequencies, or are otherwise incompatible, allowing them to exchange power without requiring the tight coordination of a synchronous network. HVDC has other advantages as well, especially for transmitting large amounts of power over very long distances. Fundamentals of both alternating current (AC) and direct current (DC) are discussed below.
General Potential Benefits of Grid Interconnections[1]
There are number of technical rationales for grid interconnections, many of which have economic components as well.
Technical rationales for grid interconnection include:
- Improving reliability and pooling reserves: The amount of reserve capacity that must be built by individual networks to ensure reliable operation when supplies are short can be reduced by sharing reserves within an interconnected network.
- Reduced investment in generating capacity: Individual systems can reduce their generating capacity requirement, or postpone the need to add new capacity, if they are able to share the generating resources of an interconnected system.
- Improving load factor and increasing load diversity: Systems operate most economically when the level of power demand is steady over time, as opposed to having high peaks. Poor load factors (the ratio of average to peak power demand) mean that utilities must construct generation capacity to meet peak requirements, but that this capacity sits idle much of the time. Systems can improve poor load factors by interconnecting to other systems with different types of loads, or loads with different daily or seasonal patterns that complement their own.
- Economies of scale in new construction: Unit costs of new generation and transmission capacity generally decline with increasing scale, up to a point. Sharing resources in an interconnected system can allow the construction of larger facilities with lower unit costs.
- Diversity of generation mix and supply security: Interconnections between systems that use different technologies and/or fuels to generate electricity provide greater security in the event that one kind of generation becomes limited (e.g., hydroelectricity in a year with little rainfall). Historically, this complementarity has been a strong incentive for interconnection between hydro-dominated systems and thermal-dominated systems. A larger and more diverse generation mix also implies more diversity in the types of forced outages that occur, improving reliability.
- Economic exchange: Interconnection allows the dispatch of the least costly generating units within the interconnected area, providing an overall cost savings that can be divided among the component systems. Alternatively, it allows inexpensive power from one system to be sold to systems with more expensive power.
- Environmental dispatch and new plant siting: Interconnections can allow generating units with lower environmental impacts to be used more, and units with higher impacts to be used less. In areas where environmental and land use constraints limit the siting of power plants, interconnections can allow new plant construction in less sensitive areas.
- Coordination of maintenance schedules: Interconnections permit planned outages of generating and transmission facilities for maintenance to be coordinated so that overall cost and reliability for the interconnected network is optimized. Some costs and benefits of interconnections are difficult to quantify, but as a rough figure of merit it has been estimated that interconnections in North America have resulted in an overall annual cost savings of $20 billion in the 1990s, and that the Western European interconnection has resulted in reduced capacity requirements of 7-10 %.
Technical Complexities and Risks of Grid Interconnections[1]
The fact that interconnections between power systems are increasingly common does not imply that they are as simple as connecting a few wires. Interconnections obviously entail the expense of constructing and operating transmission lines and substations, or in the case of HVDC, converter stations. Interconnections also entail other costs, technical complexities, and risks. For AC interconnections especially, a power system interconnection is a kind of marriage, because two systems become one in an important way when they operate in synchronism. To do this requires a high degree of technical compatibility and operational coordination, which grows in cost and complexity with the scale and inherent differences of the systems involved. To give just one example, when systems are interconnected, even if they are otherwise fully compatible, fault currents (the current that flows during a short circuit) generally increase, requiring the installation of higher capacity circuit breakers to maintain safety and reliability. To properly specify these and many other technical changes required by interconnection requires extensive planning studies, computer modeling, and exchange of data between the interconnected systems.
The difficulties of joint planning and operation of interconnected systems vary widely. As with marriages, from the institutional and administrative standpoint, coupled systems may become a single entity, or they may keep entirely separate accounts. Within the North American interconnections, for example, there are hundreds of electric utility companies that are entirely separate commercial entities. Customers receive power from, and pay bills to, the utility that serves their area, for example Consolidated Edison. They may do so without even knowing of the existence of the Eastern interconnection. Yet all the utilities in the Eastern interconnection are in a technical marriage that dictates or constrains key aspects of their technology choices and operating procedures. Within countries, there are typically common technical standards for all utilities, which reduces the complexity of interconnecting separate systems. In different countries, on the other hand, power systems may have evolved quite separately, with very different standards and technologies, which adds an extra layer of technical complexity to interconnections. Institutional and administrative features of power systems in different countries are also likely to differ in many ways, and these differences invariably affect the technical and operational dimensions of an interconnection. Issues ranging from power trading agreements to reliability standards, while expressed in technical terms, often must be resolved within the realm of policy and political economy. As one expert on international interconnections has remarked, “many technical, organizational, commercial and political problems have had to be solved to get large networks linked by international interconnections to operate”[5].
The greatest benefits of interconnection are usually derived from synchronous AC operation, but this can also entail greater reliability risks. In any synchronous network, disturbances in one location are quickly felt in other locations. After interconnecting, a system that used to be isolated from disturbances in a neighboring system is now vulnerable to those disturbances. As major blackouts in North America and Europe in 2003 demonstrated, large-scale disturbances can propagate through interconnections and result in cascading outages, bringing down systems that had previously been functioning normally. In addition, long-distance interconnections with long transmission lines have potentially greater stability problems than is the case for shorter lines. Finally, many systems that have undergone electricity liberalization in recent years have experienced large increases in transmission capacity utilization, reducing reserve margins. Minimizing the likelihood that an interconnection will lead to such problems as voltage collapse, dynamic and transient instability, or cascading outages due to propagated disturbances requires careful planning and well-coordinated operation.
Technical Parameters of Interconnection[1]
Basic Electrical Parameters
This section describes the basic electrical parameters and units of measurement used in electric power systems. It is meant to provide the non-technical reader with the concepts needed for a general understanding of the technical issues discussed in subsequent sections.
Alternating Current (AC) and Direct Current (DC)
Electric power comes in two forms:
- alternating current (AC) and
- direct current (DC).
These forms are characterized by the behavior of their waveforms: AC alternates between positive and negative polarity with respect to ground, while DC does not.
In power systems, AC is generally a sine wave, while DC is a constant value. Early electricity systems, such as Thomas Edison’s Pearl Street Station in New York City, which provided the world’s first public electric service in 1882, were DC. However, by the beginning of the 20th century AC systems had become standard worldwide. The main reason for the adoption of AC was that it is relatively simple to change AC voltage levels by using transformers, while it is difficult to change DC voltages. The development of solid-state power electronics in recent years has allowed an increased use of DC in the form of HVDC interconnections, but otherwise power systems remain AC.
Frequency (Hz)
Frequency is the rate at which an alternating current changes from positive to negative polarity, measured in cycles per second, or hertz (Hz). There are currently two widespread world standards for power system frequency: 50 Hz in most of Europe and Asia, and 60 Hz in North America and in other places strongly influenced by the U.S. power industry, such as South Korea. The choice of 50 and 60 Hz systems in different locations is a consequence of historical legacies rather than the inherent technical superiority of one or the other. However, the range of possible frequencies for power systems is constrained by practical concerns. For example, a century ago many electric railroads operated at a frequency of 25 Hz, but 25 Hz was never adopted for general use in power systems because frequencies at that level cause electric lights to flicker. At the other end of the scale, frequencies well above 60 Hz result in higher impedances, leading to unacceptably high transmission and distribution losses.
Voltage (V)
Voltage is the difference in electric potential between two points in an electric circuit. A difference in potential causes electric charges to flow from one place to another, just as a difference in heights causes water to flow from one level to another. Voltage is measured in volts (V), and sometimes in thousands of volts or kilovolts (kV). In power systems, two important measures are the maximum voltage and average voltage at any particular point. Maximum voltage is important because insulation and safety equipment must be designed to protect against the highest voltage encountered. Average voltage is important because the amount of energy supplied to an end user or lost in transmission lines is a function of the average voltage and current. For DC systems, maximum and average voltages are the same, because DC voltage doesn’t oscillate. For example, the output of a 120 V DC power supply is a continuous 120 V relative to ground, and this is both the maximum and average voltage. For AC systems, different measures are required. In a 120 V AC system, the voltage actually oscillates in a sine wave between + 170 V and – 170 V relative to ground. The maximum voltage, also called amplitude or peak voltage, is thus 170 V. The simple arithmetic average of this waveform is actually 0 V, since the positive and negative voltages cancel each other out. Hence, another type of average is used, called root-mean-square (RMS). RMS is obtained by squaring the values of the voltage over one complete sine-wave cycle, determining its average value, and then taking the square root of that average. The result (true for any sine wave) is that VRMS = VPEAK / √2 = 0.707 VPEAK. For a household system with a VPEAK = 170 V, VRMS = 0.707 (170 V) = 120 V. Thus the common designation of a household electric outlet as “120 V AC” refers to the RMS value of the voltage. The voltages of power system components, such as transformers and transmission lines, are also generally given in RMS terms.
Current (I)
Current is the flow rate of electric charge. In an electric circuit, charge flows from a point of higher voltage to a point of lower voltage through a conductor, just as water flows from a higher spot to a lower one through a pipe. Current is measured inamperes (A) or kilo-amperes (kA), where one ampere is a certain number of charges (to be precise 6.25 x 1018 charges, called one coulomb) flowing per second. As is the case for voltage, AC currents are generally described in terms of their RMS values.
Resistance (R) and Conductance
Conductance describes the ability of an object, such as an electric wire, to allow electric currents to flow. The reciprocal of conductance is resistance, which describes how much the object resists the flow of current. Resistance is measured in ohms (Ω). The resistance of wire is a product of its resistivity (an inherent property of the material from which it is made, such as copper or aluminum, for a given temperature) and the dimensions of the wire. For a given material, the longer the wire is, the greater the resistance, and the larger in diameter the wire is, the smaller the resistance. In the analogy of water flowing from a higher to a lower spot through a pipe, resistance is analogous to the friction of the pipe. A narrow pipe has a higher resistance; a wide pipe has a lower resistance.
Ohm’s Law
Ohm’s Law describes the relationship between voltage (V), current (I), and resistance (R) across any element of a DC electric circuit: V = I∗R. Thus, for a fixed value of resistance – say for an HVDC transmission line of a certain length and diameter – if the voltage is made larger, the current will decrease, and vice versa. For example, if the resistance of a line is 25 Ω, and the current through the line is 1 kA, then the voltage drop across the line is V = 1 kA * 25 Ω = 25 kV. If the voltage on the sending side was 500 kV, then the voltage on the receiving side must be 25 kV less, or 475 kV.
Power and Energy
Power is the rate of energy flow, measured in watts (W), and sometimes in thousands of watts or kilowatts (kW), or in millions of watts or megawatts (MW). For a DC circuit, the power passing through any element of the circuit (e.g. a transmission line, a generator, an electrical appliance) is the product of the voltage across it and the current passing through it: P = I∗V. The energy delivered by a power system is measured in kilowatt-hours (kWh), and sometimes megawatthours (MWh). In general, energy is equal to power times time. For example, a light bulb that draws 100 W of power and is in use for 10 hours consumes a total amount of energy, E = 0.1 kW * 10 h = 1 kWh. Note that power and energy are quite different concepts. If an electric oven draws 1 kW of power and is in use for an hour, E = 1 kW * 1 h = 1 kWh. In these two examples, the power levels are different but the energy consumed is the same, the difference being the length of time that each device is operated. Note that the basic unit of energy is the joule (J), while the basic unit of power is the watt, where 1 W = 1 J/s. Thus 1 kWh = 1 kW * 1 h = 1000 J/s * 3600 s = 3.6 million J.
Resistive Losses
When current flows against a resistance, some of its energy is lost in the form of heating. For a DC circuit, the resistive losses can be calculated using Ohm’s Law: PLOSS = I∗V = I(I/R) = I2R. To continue with the example under “Ohm’s Law” above, consider a 500 kV HVDC transmission line with 25 Ω of resistance, with 1 kA of current passing through it, and which has a voltage on the sending end of 500 kV, and a voltage on the receiving end of 475 kV. The total power being transmitted at the sending end of the transmission line is P = 500 kV ∗ 1 kA = 500 MW. Out of this 500 MW, the amount being lost to heating is PLOSS = (1 kA)2 ∗ 25 Ω = 25 MW. This constitutes 25 MW/500 MW = 5 percent of the power being transmitted. Very high voltages are used in transmission in order to reduce resistive losses to a tolerable level. In the example above, if the same amount of power were being transmitted (500 MW) but the sending voltage were 125 kV instead of 500 kV, the current through the line must be I = P/V = 500 MW/125 kV = 4 kA; the current is four times higher to yield the same amount of power, because the voltage is four times less. The power lost in the transmission line is then PLOSS = (4 kA)2 ∗ 25 Ω = 400 MW = 80 percent of the power being transmitted. In general, line losses are inversely proportional to the square of the sending voltage; this is true for AC lines as well as DC. For this reason, historically power systems have sought to increase their transmission voltages as distances and amounts of power transmitted have grown. The highest common AC transmission voltages, sometimes referred to as extra high voltage (EHV), are 380 kV in Europe and 765 kV in the US. Voltages as high as 1200 kV have been used in Russia for some long-distance lines across Siberia. Above 1000 kV, however, the practical difficulty and expense of equipment and insulation that can withstand such high voltages becomes prohibitive.
Impedance, Reactance, Inductance, Capacitance
AC circuits involve not only resistance but other physical phenomena that impede the flow of current. These are inductance and capacitance, referred to collectively as reactance. When AC currents pass through a reac tance (e.g. in transmission and distribution lines, in transformers, or in end-use equipment such as electric motors) some of the energy is temporarily stored in electro-magnetic fields.
This has three important implications:
- Even though energy is not “lost” to the environment as in the case of resistive heating, it must still be supplied to the reactive elements. This is known as reactive power.
- Voltage decreases when current flows across a reactance, just as it does across a resistance. For AC circuits, Ohm’s Law must be modified: V = I∗Z, where Z is the sum of resistance and reactance, called impedance, and is measured in ohms.
- V, I, and Z are all complex numbers, meaning that they express not only magnitudes in volts, amps, and ohms, but also phase angles.
Voltage and current waveforms both oscillate at same frequency - either 50 Hz or 60 Hz depending on the system – but they can differ in terms of the angular location within a cycle at which the maximum voltage or current occurs. This difference in angular location is referred to as phase difference, often symbolized by φ (phi) or θ (theta) and measured in degrees (or radians). Passing through an inductance causes an AC current waveform to fall behind, or lag, the voltage waveform. Passing through a capacitance causes AC current to move ahead of, or lead, the voltage. Equivalent amounts of capacitance and reactance cancel each other out.
Complex Power: Real, Reactive, Apparent
For AC systems, there are three kinds of power: real, reactive, and apparent. Real power (sometimes called active power) is what is consumed by resistances, and is measured in W (or kW, or MW). Reactive power is consumed by reactances, and is measured in volt-amperes reactive, or VAR (sometimes kVAR, or MVAR). Apparent power is the complex sum of real and reactive power, and is measured in voltamperes, or VA (or kVA or MVA). S = √(P2 + Q2), where S is apparent power, P is real power, and Q is reactive power. Apparent power is what must be supplied by the generators in a power system to meet the system’s electrical load, whereas end-use is generally measured in terms of real power only. Utilities always seek to minimize reactive power consumption, among other reasons because it is difficult to measure and be compensated for reactive power by customers.
Loads and Power Factors
An electrical load is the power drawn by an end-use device or customer connected to the power system. (Sometimes, “load” is used to refer to the end-use devices or customers themselves, but among engineers it usually refers to the power demand.) Loads can be resistive or reactive, and are often a combination of both. The extent to which a load is resistive is measured by its power factor, (p.f.), which is equal to the cosine of the phase difference between the current and voltage through the load: p.f. = cos φ. When the power factor is at its maximum value of one, the load is purely resistive. On the other hand, the smaller the power factor, the greater the phase difference and the greater the reactive power component of the load. Inductive loads, such as electric motors, have a lagging power factor (see 2.1.9), and are said to consume reactive power. Capacitive loads have a leading power factor and are said to be sources of reactive power. Given the voltages and currents through a circuit element, apparent, real, and reactive power can be calculated respectively as follows: S = IRMS * VRMS P = S * p.f. = IRMS * VRMS * cos φ Q = IRMS * VRMS * sin φ
Reactive loads can have a large effect on line losses, because the current flowing through a line, and the associated heating, is a function of the apparent power S rather than the real power P. For example, consider a load of 150 kW with a lagging power factor of 0.75, which is supplied by a 10 kV distribution line with a resistance of 10 Ω. The apparent power drawn by the load is S = P/p.f. = 150 kW/0.75 = 200 kVA. The current to the load is then I = 200 kVA/10 kV = 20 A. The line loss is PLOSS = I2 * R = (20 A)2 * 10 Ω = 4 kW. If there were no reactive power consumption by the load, the power factor would be equal to one. In that case, S = P = 150 kW. Then I = 150 kW/10 kV = 15 A, and PLOSS = (15 A)2 * 10 Ω = 2.25 kW. Thus the reactive load in this example increased the line losses from 2.25 kW to 4 kW, an increase of 78 %.
Three-Phase Systems
House current is generally single-phase AC power, but the rest of the power system from generation to secondary distribution employs 3-phase AC. This means that transmission lines have three separate conductors, each carrying one-third of the power. The waveforms of the voltage in each phase are separated by 120°.
There are two major reasons that 3-phase power became dominant:
- As long as the electrical loads on each phase are kept roughly balanced, only three wires are required to transmit power. Normally, any electric circuit requires both an “outbound” and “return” wire to make a complete circuit. Balanced 3-phase circuits provide their own return, and thus only three, rather than six, wires are required to transmit the same amount of power as three comparable single-phase systems.
- Since the invention of polyphase induction motors by Nikola Tesla in the 1890s, 3-phase motors have been the workhorse of industry. More than one phase is required to balance torque, which increases the effectiveness and lifetime of both motors and generators.
Voltage and Power in Three-Phase Systems The voltage in 3-phase systems can be specified in two different ways. One is phase to ground, which as it sounds is the voltage between any one of the three phases and ground. The other is phase to phase, which is the voltage between any two of the three phases. Power lines are conventionally described by their phase to phase voltage, also called the line voltage. Phase to phase voltage is greater than phase to ground voltage by a factor of the square root of three. Thus, a 500 kV line has a phase to phase voltage of 500 kV, and a phase to ground voltage of 500 kV/√3 = 289 kV. In both cases, the voltage referred to is the RMS value. The amount of power transmitted in a three-phase system is three times the power in each line. Thus S = 3 (I * VLINE/√3) = √3 I * VLINE, where VLINE is the phase to phase voltage. For example, the apparent power transmitted by a 500 kV circuit with a current of 1 kA is S = √3 * 500 kV * 1 kA = 866 MVA. The real and reactive components can be calculated easily if the load power factor or phase difference is known (see 2.1.10). In this example, if φ = 25°, the real power P = S cos 25° = 866 MVA * 0.906 = 785 MW, and the reactive power Q = S sin 25° = 866 MVA * 0.422 = 366 MVAR.
Basic Design Features
The basic design features of an interconnection include the following elements:
- whether it is AC or DC • if DC, whether it is single-pole or double-pole (+/-)
- transmission capacity (in MVA)
- transmission voltage (in kV)
- system components and overall design
- operating agreement
These features are dictated by the answers to the following questions:
- Will the interconnected systems operate synchronously or asynchronously? To operate synchronously, at a minimum the systems must have the same nominal frequency (50 Hz or 60 Hz). Even if frequencies are the same, technical and operational differences can make synchronous operation too difficult or expensive to pursue. Many synchronous networks with the same nominal frequency, including the four North American interconnections, have only asynchronous DC connections between them.
- What are the magnitudes and directions of the anticipated power flows? The basic rationales for the interconnection must be expressed quantitatively, using models that forecast the power flows through the interconnection among constituent systems. The forecasts must be conducted on different time scales: diurnal, seasonal, annual, and multi-year projections.
- What physical distance and terrain will the interconnection span? The peak power flows and the physical length of the interconnection will influence the choice of AC or DC, the size of conductors, and requirements for other system components, such as series capacitors or phase-shifting transformers. Terrain, geology, and land use considerations (such as urban areas, environmentally sensitive areas) will determine whether overhead lines or underground cables are used, the layout and design of substations or converter stations, grounding and lightning protection schemes, and the most suitable kinds of support structures. Undersea transmission requires the use of special cables that are quite different from terrestrial cables and overhead lines. Terrain and land use also dictate construction and maintenance methods.
- What are the key technical and operating differences among the systems to be interconnected? These include differences in the hardware, control systems, and procedures used for frequency regulation, voltage regulation, and fault protection.
Interconnection Elements
A listing of the basic elements of an interconnection is provided below. Technical Objectives The ultimate objective of an interconnection, like the power systems it is part of, is to provide power to customers economically, safely, reliably, efficiently, and with minimal environmental impact. Each of these aspects has one or more quantitative measure, such as price per kilowatt-hour, number and lethality of accidents, frequency and duration of service interruptions, generating plant heat rate, transmission and distribution losses, and emissions factors. Interconnections are designed, and their individual components selected, with all of these objectives in mind, though they may be optimized differently in different systems.
Transmission Lines
Transmission lines come in two basic varieties: overhead lines and underground (or undersea) cables. Overhead lines are more common and generally less expensive than cables. The main design consideration for overhead lines is the choice of conductor type and size, which must balance the need to minimize impedance (and the associated losses), minimize cost, and minimize the weight that must be carried by support structures. Although copper is a better conductor, it has been overtaken in recent years by aluminum, which is lighter, cheaper, and in abundant supply. The most common variety of overhead conductor for high-capacity, long-distance transmission is stranded aluminum wire reinforced with steel (known as ACSR, for “aluminum conductor steel reinforced”). Other design considerations for overhead lines are the type of support structures (such as transmission towers and insulators) used, and the configuration of conductors on the support structures, which affects the reactance of the conductors and the strength of electromagnetic fields (EMFs) around the lines. Underground cables are used where overhead conductors are inappropriate due to environmental or land use considerations, such as in high-density urban areas or ecologically sensitive areas. Cables are insulated and are typically routed through underground conduits, and often require cooling systems to dissipate heat. Cables may use copper instead of aluminum, balancing the greater cost of copper against its superior conductivity and lower resistive heating. Undersea cables are usually made of copper, and may be surrounded by oil or an oil-soaked medium, then encased in insulating material to protect from corrosion. Undersea cables often have a coaxial structure, which has an inherently high capacitive reactance; therefore undersea cables are usually DC, which is not affected by reactance. Conductor cross-sections are typically measured in square centimeters (cm2) in the metric system, or thousands of circular mils (kcmil) in the American system (1 kcmil = 0.005 cm2). The capacity of a conductor to carry current without exceeding thermal limits is called its ampacity, measured in kA for large conductors.
Support Structures
There are many possible types of support structures for overhead transmission lines. In developed countries, transmission lines are supported on structures made out of steel lattice, tubular steel, wood, and concrete. Of these, steel lattice has the highest strength to weight ratio, and is the easiest to assemble in areas that are difficult to access[6]. Where aesthetics are an important factor, however, other materials are often used. The main function of support structures is to keep the conductors from contacting trees or other objects, including people and animals; thus the structures must be tall enough to do so even when the conductors sag due to high temperatures caused by resistive heating.
All things being equal, taller structures also minimize ground-level EMFs. Because overhead transmission lines are not insulated, they are typically suspended from towers on strings of ceramic insulators, which are designed to prevent flashover, or the leakage of current from the conductors to the tower, which would present a lethal prospect to anyone touching the tower. AC transmission towers are usually designed to carry three conductors: the three phases of AC power systems. Towers that hold these in an equilateral triangle shape (called a “delta”) keep the mutual reactances of the three phases balanced; non-delta configurations often require that conductors be transposed, or switch places, at regular intervals along the transmission path. Some towers carry more than one circuit, with three phases per circuit; for example, a double-circuit tower will have six conductors. (The conductor for each phase may also be subdivided into “bundles” of two or more conductors, which are physically close together.) DC transmission towers carry two conductors per circuit. Figure 2-1 on the following page shows various options for transmission tower design.
Transformers and Substations
Transformers are used to change voltage levels in AC circuits, allowing transmission at high voltages to minimize resistive losses, and low voltages at the customer end for safety. This ability, following the development of transformers by William Stanley in 1885, led to the rapid adoption of AC systems over DC systems. The essential element of a transformer consists of two coils of wire wrapped around an iron core. An alternating current in one coil produces a changing electromagnetic field that induces a current in the other. The voltages on either side are in the same ratio as the number of turns on each coil. For example, a transformer with a 10:1 “turns ratio” that is connected to a 15 kV supply on its primary side, will have a voltage of 150 kV on its secondary side. Transformers step up the voltage from generator to transmission system, and other transformers step it down, often in several stages, from transmission to sub-transmission to primary distribution to secondary distribution, and finally to the end-user voltage, such as 120 V. At the distribution level, transformers often have taps that can be used to change the turns ratio; this allows operators to maintain customer voltage levels when system voltages change. Modern transformers are extremely efficient, typically greater than 99%, but even small losses can produce a great deal of heat, which must be dissipated to prevent damage to the equipment. Large transformers are cooled by circulating oil, which also functions as an electrical insulator.

Large transformers are housed in substations, where sections of a transmission and distribution system operating at different voltages are joined. Larger substations have a manned control room, while smaller substations often operate automatically. In addition to transformers, important substation equipment includes switchgear, circuit breakers and other protective equipment (see next section), and capacitor banks used to provide reactive power support.
Protection Systems
Protection systems are an extremely important part of any power system. Their primary function is to detect and clear faults, which are inadvertent electrical connections – that is, short circuits – between system components at different voltages. When faults occur, very high currents can result, typically 2-10 times as high as normal load currents. Since power is proportional to I2, a great deal of energy can be delivered to unintended recipients in a very short time. The goal of protection systems is to isolate and de-energize faults before they can harm personnel or cause serious damage to equipment. Note that protection systems are designed to protect the power system itself, rather than end-user equipment. The key components of protection systems are circuit breakers, instrument transformers, and relays. Circuit breakers are designed to interrupt a circuit in which high levels of current are flowing, typically within three voltage cycles (about 50 milliseconds in a 60 Hz system).
To do this they must quench the electric arc that appears when the breaker contacts are opened; this is usually accomplished by blowing a gas, such as compressed air or sulfur hexafluoride (SF6) across the contacts. Since human operators generally could not respond to a fault in time to prevent damage, circuit breakers are operated by automatic relays that sense faults or other undesirable system conditions. To distinguish between normal operations and fault conditions, relays are connected to instrument transformers – voltage transformers (VT) and current transformers (CT) – that reflect the voltages and currents of the equipment they are connected to. Relays themselves can be either electromechanical or solid state devices. Essential aspects of protection system design include determining the specifications and placement of protection equipment, and also the correct timing and sequence of relay operations. Protection engineers must determine how long an undesirable condition should be allowed to persist before opening a circuit breaker, and the order in which circuit breakers must open to correctly isolate faults in different zones[7].
Communications, Monitoring, and Control Systems
Power system operations take place within geographically well-defined control areas, which traditionally corresponded to a utility’s service territory. With market liberalization, individual utility control areas have sometimes been combined into larger control areas under the jurisdiction of an independent system operator (ISO). In either case, system operations are coordinated by a central control center, the responsibility of which it is to keep the entire system running safely and reliably. This entails continuously monitoring system conditions and deploying system resources as the situation requires. Traditionally, monitoring and control have been conducted semi-manually, with a heavy reliance on telephone communications with plant operators and field personnel.
Increasingly, these activities are automated. Supervisory control and data acquisition (SCADA) systems combine remote sensing of system conditions with remote control over operations. For example, control center SCADA systems control key generators through automatic generator control (AGC), and can change the topology of the transmission and distribution network by remotely opening or closing circuit breakers. This monitoring and control is enabled by dedicated phone systems (often fiber-optic based), microwave radio, and/or power line carrier signals
Technical Issues Associated with AC Grid Interconnection
General Requirements for AC Interconnection
AC interconnection usually provides the greatest interconnection benefits, except in certain cases for which DC is the preferred option (see Section 2.4.1). Synchronous interconnection of different systems is, however, technically demanding. At a general level, the first requirement is that the systems share the same nominal frequency, either 50 Hz or 60 Hz. Then, they must regulate frequency so that they achieve and remain in synchronism (see Section 2.3.4, below). They must also interconnect at a common voltage level. This is easier if the countries involved have agreed to a common standard for transmission voltage, such as the 380 kV standard in Europe.
It is still possible for countries with different voltage schemes to interconnect by using transformers (if voltages are not very different, autotransformers are often used, which have only a single winding and are less expensive than ordinary transformers). Having to use an excessive number of transformers is, however, undesirable, since transformers are costly, add impedance to the line, and may require lengthy repair after a fault, keeping the transmission intertie out of operation for an extended period[8]. Other, more specific technical issues are discussed in the remainder of this section. Good engineering must be complemented by good cooperation among the interconnected systems. In both planning and operation phases, this requires extensive data sharing, joint modeling, and clear communication.
Technical Issues for AC Interconnection
One way of thinking about the technical issues of AC interconnections is to group them into those associated with the transmission interconnection itself, and those associated with operating the larger interconnected system. Transmission issues are discussed in Key issues include thermal limits, stability limits, and voltage regulation, which are the main constraints on transmission line operation. Other transmission issues include loop and parallel path flows, available transfer capacity, and FACTS technologies. System-wide issues are discussed in including frequency regulation,power quality, the coordination of planning and operations, political and institutional cooperation, systems that are aging or in poor repair, and the operation of nuclear power plants. The implications of electricity market liberalization for interconnected systems are also discussed.
Transmission Issues
Thermal limits
The capacity of transmission lines, transformers, and other equipment is determined by temperature limits. If these limits are exceeded, the equipment can be damaged or destroyed. Equipment ratings have traditionally been conservative, and operators have stayed well below the rated limits, but increased power trading in liberalized markets has created pressure for higher utilization. Instead of a single thermal limit, dynamic ratings are now often used. For example, transmission lines can carry more current when heat is effectively dissipated, and thus will have a higher rating on cold, windy days without direct sunlight. When transmission lines heat up, the metal expands and the line sags. If the sag becomes too great, lines can come into contact with surrounding objects, causing a fault. Excess sag can also cause the metal to lose tensile strength due to annealing, after which it will not shrink back to its original length. Important transmission lines are often monitored by a device called a “sagometer”, which measures the amount of sag, making system operators aware of dangerous sag conditions.
Stability limits
The stability limit of a transmission line is the maximum amount of power that can be transmitted for which the system will remain synchronized if a disturbance occurs. The power flow through a transmission line is governed by the difference in power angle between the sending and receiving sides: P = VR ∗ VS ∗ sinδ / X
All other factors being equal, the power transmitted from the sending side to the receiving side increases as the difference in power angle between the two points, called δ (delta), approaches 90°, and decreases as it approaches 0°. However, the feedback mechanism that keeps generators in synchronism and returns them to synchronous operation if they are disturbed becomes more tenuous as δ approaches 90°. The stability limit represents the value of the power angle that allows the highest power transfer while maintaining stability; a typical maximum value of δ is around 45°. In general, stability limits are more important than thermal limits for long transmission lines, while thermal limits are more important for shorter lines. In the United States, for example, thermal limits are more important in the Eastern interconnection, while stability limits play a larger role in the Western interconnection.
Voltage Regulation
Utilities generally maintain system voltages within 5-10 percent of nominal values in order to avoid the risk of voltage collapse, which can lead to a major interruption of service. Power system voltages are primarily governed by reactive power flows. Voltages along a transmission link are a function of the physical length of the circuit, the impedance per unit length, and the flow of real power: the higher the current and the greater the reactance, the larger the voltage drop (if the reactance is predominantly inductive) or gain (if capacitive). Voltage collapse can be triggered when reactive demand is high and systems are operating near their stability limits, then undergo a disturbance that triggers a quick downward spiral. To maintain voltages along long AC transmission lines, reactive compensation of various kinds can be employed, such as series and shunt capacitors, and shunt reactors. (See section on FACTS, below). System operators also maintain voltage levels in order to protect end-use equipment (for example, low voltages cause motor currents to increase, and higher currents can cause thermal damage). Utilities are usually obliged to provide power to customers within prescribed voltage tolerances. Devices called tap-changing transformers in the local distribution system are used to ensure that customer voltages are maintained even when system voltages change substantially. Note, however, that the power quality experienced by the customer is generally more affected by local conditions in the distribution system, such as switching, lightning strikes, and the loads of other customers, than by conditions in the transmission system. Protecting sensitive electronic end-use equipment is the responsibility of the customer rather than the utility.
Loop and Parallel Path Flows
In power systems, power flows do not necessarily follow a specified transmission path – for example, from seller in system A to buyer in system B - but divide themselves among various connected transmission paths according to the voltage levels and impedances of the path. To put it another way, power flows conform to physical laws rather than economic agreements. In some cases, a power transaction can take quite unwanted paths, resulting in line losses and possibly overloading lines of neighbors having nothing to do economically with the transaction. In general, these phenomena are referred to as circulating power, loop flows, and parallel path flows. A well-known example of these flows is that in a power transfer from the U.S. Pacific Northwest to the state of Utah, one-third of the power flows through Southern California, and another one-third flows through Arizona.[9] What is important for the reliability of an interconnected system is that operators know the sources and destinations of all transactions and where the power will flow, and are able to calculate the resulting reliability risks (see section on power flow modeling, below).
Available Transmission Capacity (ATC)
An important measure of transmission capacity is transmission transfer capability (TTC), which is the maximum power flow that a line can accommodate at any given time and still be able to survive the loss of a major generator or transmission link elsewhere in the system. Available transmission capacity (ATC) is the TTC of a line minus the amount of capacity already committed to other uses on that line. ATC is thus the measure of how much power can be safely transmitted over a transmission line at a given time while ensuring overall system reliability.
Flexible AC Transmission System (FACTS)
Flexible AC Transmission System (FACTS) refers to a number of different technologies based on power electronics and advanced control technologies, which are used to optimize power flows and increase grid stability[10]. FACTS equipment is expensive, but it can pay for itself by directing power flows with precision, eliminating loop flows, and relieving transmission bottlenecks without requiring that new lines be built. It can also improve frequency and voltage stability, decrease transmission losses and voltage drops, and improve power quality. FACTS equipment includes static compensators, static VAR compensators, thyristor-controlled series capacitors, phase-shifting transformers, interphase power controllers, universal power flow controllers, and dynamic voltage restorers. With FACTS, AC transmission over distances that were not previously possible due to stability limits has become possible. Figure 2-2 shows, on the following page, applications for different FACTS technologies. FACTS devices have been used extensively in the North American and European interconnections, and increasingly in developing regions, including the South Africa-Zimbabwe interconnection, the Brazil north-south interconnection, and other interconnections in Latin America, Africa, and South Asia.
Transmission Upgrades
If existing transmission facilities are to be used in the interconnection but are not adequate to transmit the expected volume of power, they can be upgraded either by adding additional lines in parallel or increasing the transmission voltage. If these options are not available, FACTS or HVDC solutions can be explored.
Systems Issues
Key technical systems issues that must be addressed in planning and implementing a grid interconnection include frequency regulation, coordination of operations, interconnections of power systems with weak grids, and aspects of interconnection that are associated with electricity market liberalization. Frequency Regulation Controlling frequency in a synchronous network is ultimately an issue of precisely matching generation to load. This load-matching occurs on several time scales. System planners and operators plan generation from hours to months in advance, coordinating the dispatch of generating units and power exchanges with other systems based on factors such as historical load patterns, weather predictions, maintenance
schedules, and unplanned outages. At the scale of minutes to seconds, frequency is maintained by Automatic Generator Control (AGC), which precisely controls the real and reactive power output of certain generators that are able to respond rapidly to changes in load. Hydroelectric and gas turbine units are generally used for regulation and load following; nuclear plants and large coal-fired plants can be damaged by rapid changes of output and are not used in this function. At the instantaneous time scale, frequency synchronization is a self-regulating phenomenon. When loads suddenly increase, generators slow down slightly, giving up some of their mechanical energy of rotation to supply the additional electrical energy required; when loads suddenly decrease, generators speed up. Through feedback among the different generators in the system, synchronism is maintained, at a frequency slightly higher or lower than nominal. When the control center computers sense these frequency movements, AGCs are notified to increase or decrease generator output to the amount necessary to balance load and return frequency to nominal levels. System operators also have a variety of off-line reserves or “ancillary services” available upon need to assist in frequency regulation and other aspects of reliable system operation. The theory of parallel operation of generators in large networks, once a daunting engineering problem, was established in the 1930s. Modern networks seldom deviate from nominal frequency by more than 0.1 Hz, and generally operate within 0.01 Hz of nominal. In an interconnected system, except where DC links are used, frequency synchronization must be accomplished through the means above, jointly administered across the interconnected systems.
Coordinating Operations
The basic geographical unit of a power system is the control area, which typically has a single control center responsible for monitoring system conditions and scheduling the dispatch of all generation. In interconnected systems, transmission lines to neighboring control areas are metered and the incoming and outgoing power flows are scheduled and continuously monitored. A continuous record of the balance of load, generation, and exchanges with other control areas called the Area Control Error (ACE) is used to plan real-time corrections to maintain load-generation balance. Interconnections create a number of coordination challenges, both institutional and technical. For example, reliability standards and constraints may differ, and there may be differences in regulation and control schemes and technologies. It is important for the operators and planners of interconnected systems to be aware of the conditions and practices in their neighboring control areas. Good communication between different system operators is important for agreeing on and coordinating interchange schedules, transmission loading, maintenance schedules, procedures for fault clearing, and emergency protocols[11]. As interconnected systems expand to encompass large geographical scales, technology is striving to keep up with the associated complexities and risks.
Some important trends in grid technologies related to the problems of maintaining reliability in large AC systems include[12]:
- Faster physical control over the system, for example FACTS technologies with solid state controls that allow rapid adjustment of reactive power flows.
- Improved real-time monitoring ability, for example the development of wide area monitoring systems (WAMS).
- Faster analytical capability to complement improved monitoring.
- Improved communications.
Interconnection of Power Systems with Weak Grids
Not all interconnections take place between power systems in top technical condition. In the developing world, many power systems bear the marks of age, poor repair, and insufficient investment, ranging from corroded conductors and deteriorating insulation to leaking transformers, worn out switchgear, and a variety of inoperable equipment. Equipment is often obsolete, and operations that are automated elsewhere may be carried out manually. Systems in poor repair generally perform poorly, have serious reliability problems, and often fail to comply with safety or environmental standards. As one scholar described the difficulties of interconnection among sparse, poorly maintained systems:
“ The vastness of the area and the low power consumption density in most African countries makes the operation of the interconnection difficult from an operational point. Many of the loads are connected to spurs off a grid that has a low level of interconnectivity. In addition, most of the networks have suffered from a lack of maintenance due to a shortage of funds. This has dramatically reduced the reliability of the system and outages frequently occur in many places. The combination of these factors has forced industries to provide their own generating facilities in the form of diesel power. These plants then operate in island mode and will often also provide power to towns and villages in the immediate vicinity of the plant. Some utilities are discouraging this practice, but need to convince these clients to connect to a grid that may not be that reliable in the first place, particularly in areas connected to spurs.”[13]
Interconnection can improve such systems, by providing emergency reserves and more reliable supplies. However, careful planning must ensure that the interconnection doesn’t lead to additional stresses elsewhere in the interconnected system. Countries with weak or isolated grids are usually poor candidates for siting nuclear power plants (NPP). NPPs have much more stringent requirements regarding grid stability than do fossil fuel thermal plants, for two reasons. First, the auxiliary systems in a NPP are much more sensitive to power conditions than such systems at other plants because of the potential consequences – namely, that a major failure could lead to a nuclear accident. Second, NPPs have large amounts of decay heat to remove long after the chain reaction is shut down, and require power to operate cooling water pumps during this extended period. With weak grids, large variations in voltage and frequency will trip a NPP off-line; worse, the sudden loss of a large power plant start a cascading failure that collapses the grid altogether. With interconnection to other grids, however, siting a NPP in a country with a weak or isolated grid becomes a plausible option. The interconnection can help to stabilize the weak grid, and it can also provide access to an independent back-up grid connection, which is a safety requirement for NPPs[14].
Interconnections and Electricity Market Liberalization
Electricity market liberalization presents a combination of opportunities, challenges, and risks for interconnection projects. From the economic standpoint, the opportunity of greater access to lower-cost supplies is balanced against the challenge of operating competitive markets and the risk of market breakdowns of the type that occurred in California in 2000-2001. From the technical standpoint, the focus is on the impact of liberalization on reliability[15].
Some of the main concerns that have been raised include:
- Increased or excessive utilization of transmission capacity, reducing reliability margins
- Reduced information exchange among system operators due to proprietary concerns in a competitive environment
- Reduced investment in reliability as companies cut costs due to competitive pressures, a concern for transmission especially as generation and distribution are liberalized
- Increased complexity in planning and operations as the number of players and transactions increases, and dispatch is based on changing market prices
- The intentional creation of congestion, or the appearance of congestion, on transmission lines to drive up prices, as done by Enron and others during the California crisis
- Transaction costs associated with replacing experienced organizations and procedures with new ones as ISOs and TRANSCOs replace integrated utility control areas
Requirements for successful interconnection operation in a liberalized, more market-driven electricity sector environment include[16]:
- Make knowledge of all transactions available to system operators
- Improve cooperation between network managers of different countries
- Improve incentives for investing in infrastructure
- Clearly define the rights and obligations of all parties
- Monitor behavior and rigorously enforce rule
Further Information
- Grid Portal on energypedia
- Rural Electrification - Minimum Safety Standards for Household Connection
- Permissible Voltage Drop
- Grid Interconnection of Micro-hydro Projects (MHPs) in Nepal
References
This information is originally from the chapter Technical Aspects of Grid Interconnection, published in UN DESA (2006): Multi Dimensional Issues in International Electric Power Grid Interconnections.
- ↑ 1.0 1.1 1.2 1.3 Technical Aspects of Grid Interconnection - http://www.un.org/esa/sustdev/publications/energy/chapter2.pdf,
- ↑ T. Hughes (983),Networks of Power: Electrification in Western Society, 1880-1930, Johns Hopkins University, Baltimore, MD
- ↑ Rincliffe, R.G. (967), “Planning and Operation of a Large Power Pool.”.IEEE Spectrum: 9-96. January 967. The PJM (Pennsylvania/New Jersey/Maryland) grid was next to be developed, in 927.
- ↑ F. Meslier (999), “Historical Background and Lessons for the Future,” in J. Casazza and G. Loehr, The Evolution of Electric Power Transmission Under Deregulation , IEEE, Piscataway, NJ; pp. 28-3fckLR.
- ↑ F. Meslier (999), “Historical Background and Lessons for the Future,” in J. Casazza and G. Loehr, The Evolution of Electric Power Transmission Under Deregulation , IEEE, Piscataway, NJ; p. 32
- ↑ John Reason, “Special Report: Transmission Structures,”Electrical World, 206, 3 (March 992), pp. 3-49
- ↑ J. Blackburn (998), Protective Relaying: Principles and Applications , 2nd ed. Marcel Dekker, New York.
- ↑ Charles Concordia (999), IEEE Power Engineering Review, Feb. 999; p.7-8
- ↑ John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World, April 998, p.63
- ↑ A. Edris (2000), “FACTS Technology Development: An Update,”fckLRIEEE Power Engineering Review, March 2000
- ↑ John Casazza (998), “Blackouts: Is the Risk Increasing?”. Electrical World , April 998, p.62
- ↑ Karl Stahlkopf and Philip Sharp (998), “Reliability in Power Delivery: Where Technology and Politics Meet,”Public Utilities Fortnightly, January5,998
- ↑ Jan A de Kock (2004), “Status of International Interconnections and Electricity Deregulation in Africa”.fckLRP. 77 in IEEE Power Engineering Society Energy Development and Power Generating Committee, PanelfckLRSession: Status of International Interconnections and Electricity Deregulation in Africa , Proceedings of IEEEfckLR2004 General Meeting, Denver, 6-2 June 2004. Available as 2004GM_Africa.pdf from http://www.ewh.fckLRieee.org/cmte/ips/index.html
- ↑ John Bickel (200), Grid Stability and Safety Issues Associated with Nuclear Power Plants . Paper prepared forfckLRthe Workshop on Grid Interconnections in Northeast Asia, May 4, 200, and available as http://nautilus.org/archives/energy/grid/papers/Bickel.pdf
- ↑ George C. Loehr (998), “Ten Myths about Electric Deregulation”.fckLRPublic Utilities Fortnightly , April 15, 1998
- ↑ F. Meslier (1999), “Historical Background and Lessons for the Future,” in J. Casazza and G. Loehr, The Evolution of Electric Power Transmission Under Deregulation , IEEE, Piscataway, NJ; p.37